��Ŀ����
17��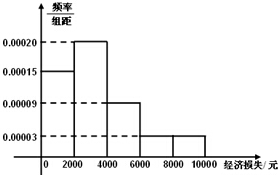 2014��7��18��15ʱ����ǿ̨�硰����ѷ����½����ʡ����ͳ�ƣ�����̨�����ȫʡֱ�Ӿ�����ʧ119.52��Ԫ���ʷ���٣�С������ס���Լ�С����50����������̨����ɵľ�����ʧ����������Ƶ�ʷֲ�ֱ��ͼ����ͼ����
2014��7��18��15ʱ����ǿ̨�硰����ѷ����½����ʡ����ͳ�ƣ�����̨�����ȫʡֱ�Ӿ�����ʧ119.52��Ԫ���ʷ���٣�С������ס���Լ�С����50����������̨����ɵľ�����ʧ����������Ƶ�ʷֲ�ֱ��ͼ����ͼ������һ��
| ������ʧ4000Ԫ���� | ������ʧ4000Ԫ���� | �ϼ� | |
| ����500Ԫ | 30 | 9 | 39 |
| ������500Ԫ | 5 | 6 | 11 |
| �ϼ� | 35 | 15 | 50 |
����̨�����ί�����С������Ϊ̨����������С�������50������������1���ڱ�1����հ״���д��ȷ���֣���˵���Ƿ���95%���ϵİ�����Ϊ��������Ƿ���ڻ�����500Ԫ������������ʧ�Ƿ�4000Ԫ�йأ�
����̨�������С��������Ŵ�����С�����о�����Ŵ�������ʦ������ʦ�����˽���ά�ޣ���ʦ��ÿ��������7��00��8��00֮�������ʱ������С������ʦ��ÿ��������7��30��8��30��֮�������ʱ������С����������3���ڣ���2����ʦ������ʦ���絽С���ĸ��ʣ�
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| P��K2��k0�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
���� ������Ƶ�ʷֲ�ֱ��ͼ�����ɹ���С��ƽ��ÿ�������ƽ����ʧ��
�������K2�����ٽ�ֵ�Ƚϣ����ɵó����ۣ�
���������ʦ������ʦ���絽С���ĸ��ʣ�����������3���ڣ���2����ʦ������ʦ���絽С���ĸ��ʣ�
��� �⣺����ÿ�������ƽ����ʧΪ$\overline x$Ԫ����$\overline x$=��1000��0.00015+3000��0.0002+5000��0.00009+7000��0.00003+9000��0.00003����2000=3360------��3�֣�
������ͼ��
| ������ʧ4000Ԫ���� | ������ʧ4000Ԫ���� | �ϼ� | |
| ����500Ԫ | 30 | 9 | 39 |
| ������500Ԫ | 5 | 6 | 11 |
| �ϼ� | 35 | 15 | 50 |
������95%���ϵİ�����Ϊ��������Ƿ���ڻ�����500Ԫ������������ʧ�Ƿ�4000Ԫ�йأ�-----��6�֣�
��������ʦ������ʦ����С����ʱ��ֱ�Ϊx��y����x��y�����Կ���ƽ���еĵ㣮�����ȫ����������ɵ�����Ϊ��={��x��y��|7��x��8��7.5��y��8.5}����S��=1���¼�A��ʾ��ʦ������ʦ���絽С���������ɵ�����ΪA={��x��y��|y��x��7��x��8��7.5��y��8.5}����ͼ�е���Ӱ���֣�
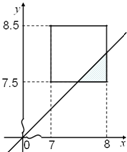
���Ϊ${S_A}=1-\frac{1}{2}��\frac{1}{2}��\frac{1}{2}=\frac{7}{8}$������$P��A��=\frac{S_A}{S_��}=\frac{7}{8}$��-----------------------------��10�֣�
�¼�B��ʾ����3���ڣ���2����ʦ������ʦ���絽С���ĸ��ʣ���$P��B��=C_3^2{��\frac{7}{8}��^2}��\frac{1}{8}��=\frac{147}{512}$---------��12�֣�
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ�������Լ���֪ʶ�����鼸�θ��ͣ�����ѧ��������������������֪ʶ�ۺ���ǿ��

��ϰ��ϵ�д�
�����Ŀ
8����֪��ABC�У���C=$\frac{��}{2}$����A����B����C��Ӧ�ı߷ֱ�Ϊa��b��c����ֱ��ax+by+c=0��Բx2+y2=4���صõ��ҳ�Ϊ��������
| A�� | 1 | B�� | 2 | C�� | $\sqrt{3}$ | D�� | 2$\sqrt{3}$ |
5����֪FΪ������y2=x�Ľ��㣬��A��B�ڸ�����������λ��x������࣬$\overrightarrow{OA}$•$\overrightarrow{OB}$=6������OΪ����ԭ�㣩�����ABO���AFO���֮�͵���Сֵ�ǣ�������
| A�� | $\frac{{17\sqrt{2}}}{8}$ | B�� | 3 | C�� | $\frac{{3\sqrt{3}}}{8}$ | D�� | $\frac{{3\sqrt{13}}}{2}$ |
2���輯��M={x|-2��x��3}��P={x|x��-1}����ô��x��M��x��P���ǡ�x��M��P���ģ�������
| A�� | ��Ҫ��������� | B�� | ��ֲ���Ҫ���� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
9����֪˫����mx2+ny2=1��������Ϊ2�����е�һ��������������y2=4x�Ľ��㣬���˫���ߵĽ����߷����ǣ�������
| A�� | $y=��\frac{3}{2}x$ | B�� | $y=��\frac{{\sqrt{3}}}{2}x$ | C�� | $y=��\frac{{\sqrt{3}}}{3}x$ | D�� | $y=��\sqrt{3}x$ |
6����˫����$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1��{a��0��b��0}��$�����ҽ���ֱ�ΪF1��F2���߶�F1F2��������y2=4bx�Ľ���ֳ�5��3���Σ����˫���ߵĽ�����Ϊ��������
| A�� | 3x��5y=0 | B�� | 5x��3y=0 | C�� | $x��\sqrt{15}y=0$ | D�� | $\sqrt{15}x��y=0$ |