题目内容
若数列{an}为等差数列,a15=8,a60=20,则a75=____________.
24
解法一:∵a15=a1+14d,a60=a1+59d,
∴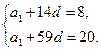
解得a1=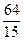 ,d=
,d=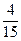 .
.
∴a75=a1+74d=24.
解法二:∵{an}为等差数列,
∴a15,a30,a45,a60,a75也成等差数列.
设其公差为d′,则a15为首项,a60为第4项.
∴a60=a15+3d′,即20=8+3d′,解得d′=4.
∴a75=a60+d′=24.
解法三:∵a60=a15+(60-15)d,
∴d=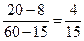 .
.
∴a75=a60+(75-60)d=24.
∴
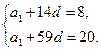
解得a1=
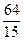 ,d=
,d=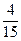 .
.∴a75=a1+74d=24.
解法二:∵{an}为等差数列,
∴a15,a30,a45,a60,a75也成等差数列.
设其公差为d′,则a15为首项,a60为第4项.
∴a60=a15+3d′,即20=8+3d′,解得d′=4.
∴a75=a60+d′=24.
解法三:∵a60=a15+(60-15)d,
∴d=
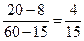 .
.∴a75=a60+(75-60)d=24.

练习册系列答案
相关题目
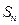 是等差数列
是等差数列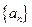 的前
的前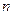 项和,且
项和,且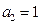 ,
,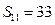 .
.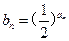 ,求证:数列
,求证:数列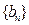 为等比数列,并求数列
为等比数列,并求数列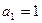 ,当
,当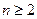 时,其前
时,其前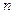 项和
项和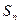 满足
满足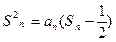
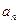 ;
;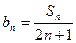 ,求数列{
,求数列{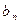 }的前项和
}的前项和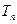
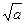 、
、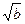 、
、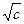 也成等差数列,则△ABC的形状为________________.
也成等差数列,则△ABC的形状为________________.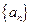 定义如下:
定义如下: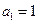 ,且当
,且当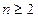 时,
时,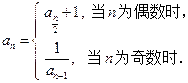
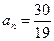 ,求正整数n.
,求正整数n.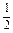 an-30,求数列{bn}的前n项和的最小值.
an-30,求数列{bn}的前n项和的最小值.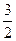 n2+
n2+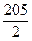 n,求数列{an}的通项公式.
n,求数列{an}的通项公式.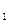
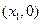 ,M
,M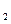
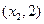 ,…,M
,…,M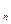
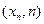 ,…,且
,…,且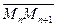 与
与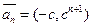
 垂直,其中是不等于零的实常数,是正整数,设
垂直,其中是不等于零的实常数,是正整数,设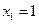 ,求数列
,求数列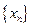 的通项公式,并求其前n项和S
的通项公式,并求其前n项和S