题目内容
已知数列{an}的前n项和为Sn=-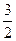
n2+
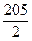n，求数列{an}的通项公式．
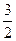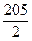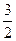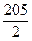n2+n，求数列{an}的通项公式．当n=1时，a1=S1=-n2+=101．
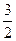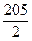当n≥2时，an=Sn-Sn-1=（-n2+n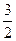）-［-（n-1）2+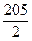（n-1）］=-3n+104．
∵a1也适合an=-3n+104，
∴数列{an}的通项公式为an=-3n+104（n∈N*）．
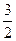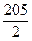n2+=101．当n≥2时，an=Sn-Sn-1=（-
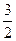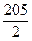n2+n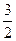）-［-（n-1）2+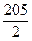（n-1）］=-3n+104．∵a1也适合an=-3n+104，
∴数列{an}的通项公式为an=-3n+104（n∈N*）．
由an与Sn的关系求通项公式是一类重要题型，要注意分类讨论的必要性．确保a1也符合所得的通项Sn.∵Sn-Sn-1=an，可用通项和前n项和的关系解决此问题，a1项要单独求解．
练习册系列答案
相关题目
17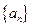
是由正数组成的数列，其前n项和为
，且满足关系：
（2）求
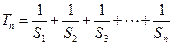
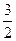n2+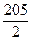
n，试求出数列{|an|}的前n项和Tn．
,问这个数列是等差数列吗？若是等差数列,其首项与公差分别是多少？
，求Sn.