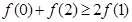题目内容
(本小题满分14分)设函数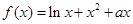 。
。
(1)若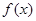 在
在 处取得极值,求
处取得极值,求 的值;
的值;
(2)若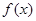 在定义域内为增函数,求
在定义域内为增函数,求 的取值范围;
的取值范围;
(3)设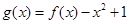 ,当
,当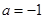 时,
时,
求证:① 在其定义域内恒成立;
在其定义域内恒成立;
求证:② 。
。
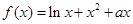 。
。 (1)若
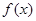 在
在 处取得极值,求
处取得极值,求 的值;
的值;(2)若
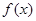 在定义域内为增函数,求
在定义域内为增函数,求 的取值范围;
的取值范围;(3)设
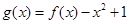 ,当
,当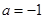 时,
时,求证:①
 在其定义域内恒成立;
在其定义域内恒成立;求证:②
 。
。(1) 。(2)
。(2)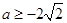 。经检验适合。(3)见解析。
。经检验适合。(3)见解析。
 。(2)
。(2)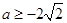 。经检验适合。(3)见解析。
。经检验适合。(3)见解析。本题以函数为载体.主要考查了了利用导数研究函数的极值,以及利用导数研究函数的单调性和不等式的证明,属于中档题
(1)先求函数的导函数,根据若x= 时,f(x)取得极值得f′(
时,f(x)取得极值得f′(  )=0,解之即可;
)=0,解之即可;
(2)f(x)在其定义域内为增函数可转化成只需在(0,+∞)内有2x2+ax+1≥0恒成立,建立不等关系,解之即可;
(3)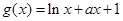 ,当
,当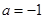 时,
时,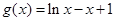 ,
,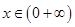 ,
,
∴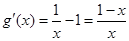
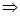
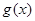 在
在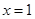 处取得极大值,也是最大值,
处取得极大值,也是最大值, 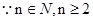 ,∴
,∴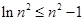 ,∴
,∴ 放缩法得到结论。
放缩法得到结论。
解:(1)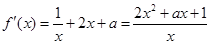 ,…………………………1分
,…………………………1分
∵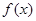 在
在 处取得极值,∴
处取得极值,∴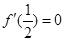 ,即
,即 。经检验适合。…………3分
。经检验适合。…………3分
(2)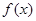 在定义域为
在定义域为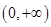 ,…………………………4分
,…………………………4分
要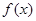 在定义域内为增函数,则
在定义域内为增函数,则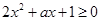 在
在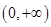 上恒成立。
上恒成立。
∴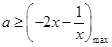 ,………………………5分
,………………………5分
而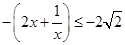 ,∴
,∴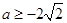 。经检验适合。…………………………6分
。经检验适合。…………………………6分
(3)①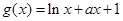 ,当
,当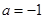 时,
时,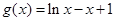 ,
,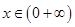 ,
,
∴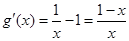 …………………………7分
…………………………7分
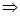
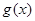 在
在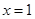 处取得极大值,也是最大值。
处取得极大值,也是最大值。
而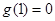 ,∴
,∴ ,在
,在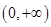 上恒成立,
上恒成立,
因此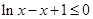 ,∴
,∴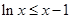 。………………………9分
。………………………9分
②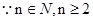 ,∴
,∴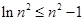 ,∴
,∴ ………………………10分
………………………10分
∴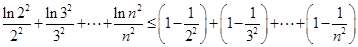
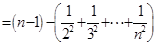 …………………………11分
…………………………11分
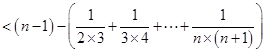 …………………………12分
…………………………12分
=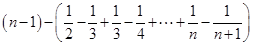
=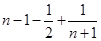 =
= 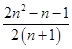 ………………………14分
………………………14分
(1)先求函数的导函数,根据若x=
 时,f(x)取得极值得f′(
时,f(x)取得极值得f′(  )=0,解之即可;
)=0,解之即可;(2)f(x)在其定义域内为增函数可转化成只需在(0,+∞)内有2x2+ax+1≥0恒成立,建立不等关系,解之即可;
(3)
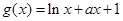 ,当
,当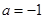 时,
时,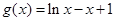 ,
,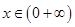 ,
,∴
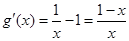
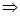
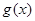 在
在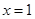 处取得极大值,也是最大值,
处取得极大值,也是最大值, 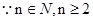 ,∴
,∴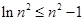 ,∴
,∴ 放缩法得到结论。
放缩法得到结论。解:(1)
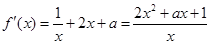 ,…………………………1分
,…………………………1分∵
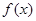 在
在 处取得极值,∴
处取得极值,∴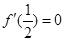 ,即
,即 。经检验适合。…………3分
。经检验适合。…………3分(2)
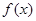 在定义域为
在定义域为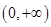 ,…………………………4分
,…………………………4分要
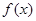 在定义域内为增函数,则
在定义域内为增函数,则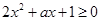 在
在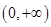 上恒成立。
上恒成立。∴
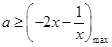 ,………………………5分
,………………………5分而
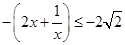 ,∴
,∴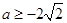 。经检验适合。…………………………6分
。经检验适合。…………………………6分(3)①
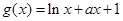 ,当
,当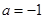 时,
时,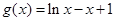 ,
,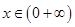 ,
,∴
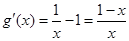 …………………………7分
…………………………7分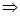
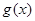 在
在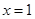 处取得极大值,也是最大值。
处取得极大值,也是最大值。而
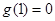 ,∴
,∴ ,在
,在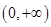 上恒成立,
上恒成立,因此
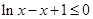 ,∴
,∴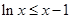 。………………………9分
。………………………9分②
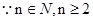 ,∴
,∴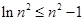 ,∴
,∴ ………………………10分
………………………10分∴
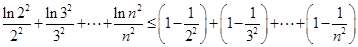
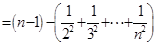 …………………………11分
…………………………11分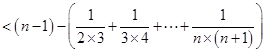 …………………………12分
…………………………12分=
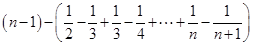
=
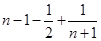 =
= 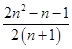 ………………………14分
………………………14分
练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 是定义在
是定义在 上的奇函数,函数
上的奇函数,函数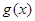 与
与 轴对称,且当
轴对称,且当 时,
时, .
. 上任意的
上任意的 ,都有
,都有 成立,求实数
成立,求实数 的取值范围.
的取值范围.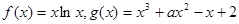
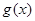 的单调递减区间为
的单调递减区间为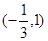 ,求函数
,求函数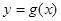 的图像在点
的图像在点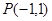 处的切线方程;
处的切线方程;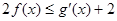 恒成立,求实数
恒成立,求实数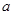 的取值范围.
的取值范围. 在点
在点 的切线方程为
的切线方程为 .
. 的解析式;
的解析式; ,求证:
,求证: 在
在 上恒成立.
上恒成立.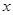 ,
,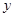 满足
满足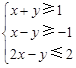 且
且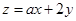 仅在点
仅在点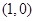 处取得最小值,则
处取得最小值,则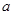 的取值范围是( )
的取值范围是( )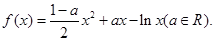 (Ⅰ) 当
(Ⅰ) 当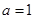 时,求函数
时,求函数 的极值;
的极值;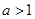 时,讨论函数
时,讨论函数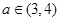 及任意
及任意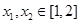 ,恒有
,恒有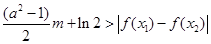 成立,求实数
成立,求实数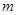 的取值范围.
的取值范围. 则 ? ?
则 ? ? 为f(x)的极大值点
为f(x)的极大值点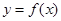 可导,
可导,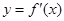 的图像可能为( )
的图像可能为( )
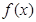 ,若满足
,若满足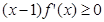 ,则必有( )
,则必有( )
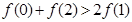
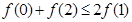 D.
D.