题目内容
(本小题满分16分)已知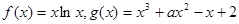
(I)如果函数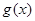 的单调递减区间为
的单调递减区间为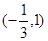 ,求函数
,求函数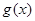 的解析式;
的解析式;
(II)在(Ⅰ)的条件下,求函数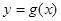 的图像在点
的图像在点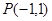 处的切线方程;
处的切线方程;
(III)若不等式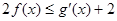 恒成立,求实数
恒成立,求实数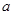 的取值范围.
的取值范围.
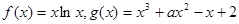
(I)如果函数
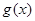 的单调递减区间为
的单调递减区间为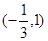 ,求函数
,求函数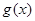 的解析式;
的解析式;(II)在(Ⅰ)的条件下,求函数
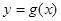 的图像在点
的图像在点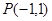 处的切线方程;
处的切线方程;(III)若不等式
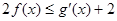 恒成立,求实数
恒成立,求实数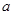 的取值范围.
的取值范围.(1)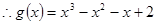 . (2)
. (2) 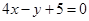 .
.
(3)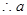 的取值范围是
的取值范围是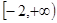 .
.
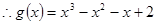 . (2)
. (2) 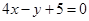 .
. (3)
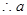 的取值范围是
的取值范围是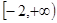 .
. (I)由题意可知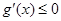 的解集为
的解集为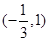 ,所以
,所以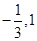 是方程
是方程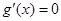 的两个根,再根据韦达定理可求出a的值.从而g(x)的解析式确定.
的两个根,再根据韦达定理可求出a的值.从而g(x)的解析式确定.
(II)由(I)得可求出 ,即点P处切线的斜率,再写出点斜式方程,转化为一般式即可.
,即点P处切线的斜率,再写出点斜式方程,转化为一般式即可.
(III)解本小题的关键此不等式 就是
就是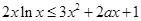 对
对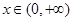 上恒成立,即
上恒成立,即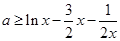 对
对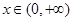 上恒成立,
上恒成立,
然后再构造函数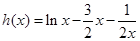 ,利用导数求其最大值即可.
,利用导数求其最大值即可.
(1)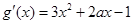 由题意
由题意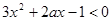 的解集是
的解集是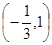
即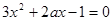 的两根分别是
的两根分别是 .
.
将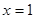 或
或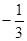 代入方程
代入方程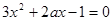 得
得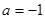 .
.
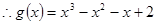 . …………5分
. …………5分
(2)由(Ⅰ)知: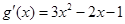 ,
,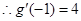 ,
,
 点
点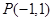 处的切线斜率
处的切线斜率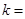
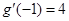 ,
,
 函数y=
函数y=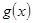 的图像在点
的图像在点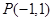 处的切线方程为:
处的切线方程为:
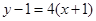 ,即
,即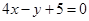 . …………10分
. …………10分
(3)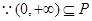 ,
,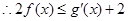
即: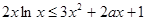 对
对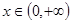 上恒成立
上恒成立
可得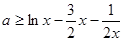 对
对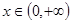 上恒成立
上恒成立
设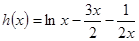 , 则
, 则
令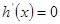 ,得
,得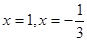 (舍)
(舍)
当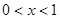 时,
时,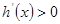 ;当
;当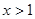 时,
时, 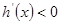
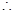 当
当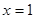 时,
时,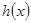 取得最大值,
取得最大值, 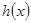
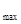 =-2
=-2 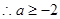 .
.
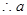 的取值范围是
的取值范围是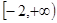 . …………16分
. …………16分
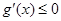 的解集为
的解集为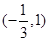 ,所以
,所以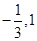 是方程
是方程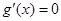 的两个根,再根据韦达定理可求出a的值.从而g(x)的解析式确定.
的两个根,再根据韦达定理可求出a的值.从而g(x)的解析式确定.(II)由(I)得可求出
 ,即点P处切线的斜率,再写出点斜式方程,转化为一般式即可.
,即点P处切线的斜率,再写出点斜式方程,转化为一般式即可. (III)解本小题的关键此不等式
 就是
就是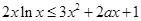 对
对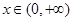 上恒成立,即
上恒成立,即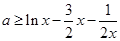 对
对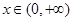 上恒成立,
上恒成立,然后再构造函数
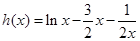 ,利用导数求其最大值即可.
,利用导数求其最大值即可.(1)
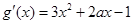 由题意
由题意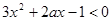 的解集是
的解集是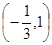
即
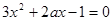 的两根分别是
的两根分别是 .
.将
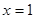 或
或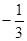 代入方程
代入方程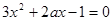 得
得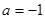 .
. 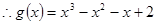 . …………5分
. …………5分(2)由(Ⅰ)知:
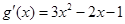 ,
,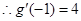 ,
,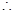 点
点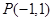 处的切线斜率
处的切线斜率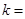
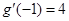 ,
, 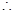 函数y=
函数y=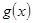 的图像在点
的图像在点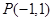 处的切线方程为:
处的切线方程为: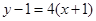 ,即
,即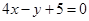 . …………10分
. …………10分(3)
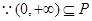 ,
,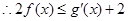
即:
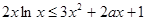 对
对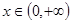 上恒成立
上恒成立 可得
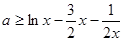 对
对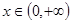 上恒成立
上恒成立设
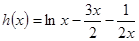 , 则
, 则
令
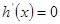 ,得
,得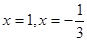 (舍)
(舍)当
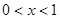 时,
时,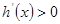 ;当
;当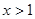 时,
时, 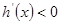
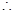 当
当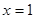 时,
时,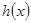 取得最大值,
取得最大值, 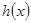
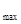 =-2
=-2 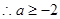 .
.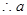 的取值范围是
的取值范围是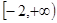 . …………16分
. …………16分
练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
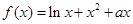 。
。 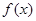 在
在 处取得极值,求
处取得极值,求 的值;
的值;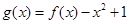 ,当
,当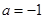 时,
时, 在其定义域内恒成立;
在其定义域内恒成立; 。
。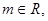 函数
函数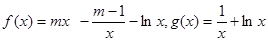
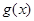 的最小值;
的最小值; 在
在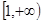 上为单调增函数,求实数
上为单调增函数,求实数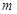 的取值范围;
的取值范围;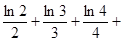 …
…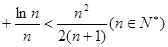 .
. .
.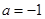 ,求函数
,求函数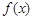 的单调增区间;
的单调增区间;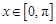 时,函数
时,函数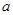 ,
,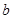 的值.
的值.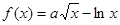
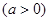
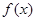 在
在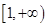 上递增,求
上递增,求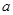 的取值范围;
的取值范围;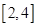 上的存在单调递减区间 ,求
上的存在单调递减区间 ,求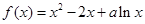 。
。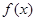 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数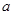 的取值范围;
的取值范围; 的导函数是
的导函数是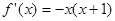 ,则函数
,则函数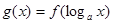
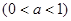

 ,
,

 ,
,