题目内容
若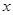 ,
,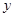 满足
满足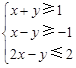 且
且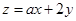 仅在点
仅在点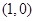 处取得最小值,则
处取得最小值,则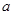 的取值范围是( )
的取值范围是( )
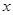 ,
,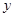 满足
满足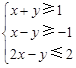 且
且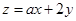 仅在点
仅在点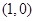 处取得最小值,则
处取得最小值,则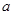 的取值范围是( )
的取值范围是( )| A.(-1,2) | B.(-2,4) | C.(-4,0] | D.(-4,2) |
D
|
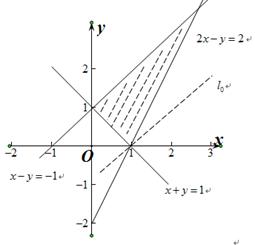
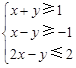 的平面区域是图中的三角形(阴影部分),又目标函数
的平面区域是图中的三角形(阴影部分),又目标函数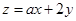 仅在点
仅在点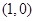 处取得最
处取得最小值,∴
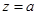 ,∴
,∴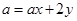 ,即
,即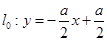 ,
,∴
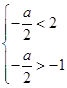 ,解得
,解得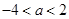 .
.点评: 本题的关键是比较直线
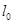 的斜率与直线
的斜率与直线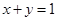 与
与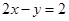 得斜率的大小.
得斜率的大小.
练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
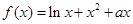 。
。 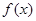 在
在 处取得极值,求
处取得极值,求 的值;
的值;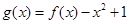 ,当
,当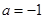 时,
时, 在其定义域内恒成立;
在其定义域内恒成立; 。
。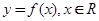 ,的导函数为
,的导函数为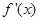 ,且
,且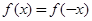 ,
,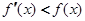 ,则下列不等式成立的是(注:e为自然对数的底数)( )
,则下列不等式成立的是(注:e为自然对数的底数)( )



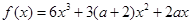 .
.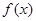 的两个极值点为
的两个极值点为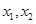 ,且
,且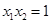 ,求实数
,求实数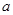 的值;
的值;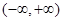 上的单调函数?若存在,求出
上的单调函数?若存在,求出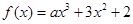 ,若
,若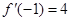 ,则
,则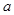 的值等于( )
的值等于( )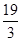


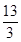
 .
.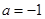 ,求函数
,求函数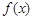 的单调增区间;
的单调增区间;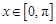 时,函数
时,函数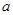 ,
,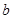 的值.
的值. .
. ,求
,求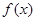 的最小值;
的最小值; ,讨论函数
,讨论函数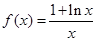 。
。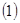 如果
如果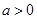 ,函数在区间
,函数在区间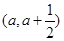 上存在极值,求实数a的取值范围;
上存在极值,求实数a的取值范围;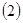 当
当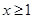 时,不等式
时,不等式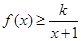 恒成立,求实数k的取值范围。
恒成立,求实数k的取值范围。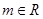 ,函数
,函数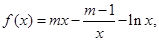
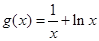 .
.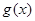 的极值;
的极值;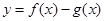 在
在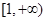 上为单调递增函数,求
上为单调递增函数,求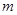 的取值范围;
的取值范围;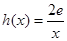 ,若在
,若在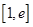 (
(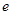 是自然对数的底数)上至少存在一个
是自然对数的底数)上至少存在一个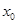 ,使得
,使得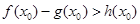 成立,求
成立,求