题目内容
(本题满分12分)
设 是定义在
是定义在 上的奇函数,函数
上的奇函数,函数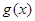 与
与 的图象关于
的图象关于 轴对称,且当
轴对称,且当 时,
时, .
.
(I)求函数 的解析式;
的解析式;
(II)若对于区间 上任意的
上任意的 ,都有
,都有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
设
 是定义在
是定义在 上的奇函数,函数
上的奇函数,函数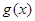 与
与 的图象关于
的图象关于 轴对称,且当
轴对称,且当 时,
时, .
.(I)求函数
 的解析式;
的解析式;(II)若对于区间
 上任意的
上任意的 ,都有
,都有 成立,求实数
成立,求实数 的取值范围.
的取值范围.(1)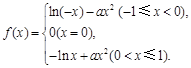 ;
;
(2),实数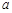 的取值范围为
的取值范围为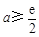 .
.
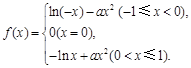 ;
;(2),实数
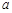 的取值范围为
的取值范围为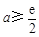 .
.本题主要考查函数恒成立问题以及函数解析式的求解及常用方法和奇偶函数图象的对称性,是对函数知识的综合考查,属于中档题.
(1)先利用函数g(x)与f(x)的图象关于y轴对称得:f(x)的图象上任意一点P(x,y)关于y轴对称的对称点Q(-x,y)在g(x)的图象上;然后再利用x∈[-1,0)时,-x∈(0,1],则f(x)=g(-x)求出一段解析式,再利用定义域内有0,可得f(0)=0;最后利用其为奇函数可求x∈(0,1]时对应的解析式,综合即可求函数f(x)的解析式;
(2)先求出f(x)在(0,1]上的导函数,利用其导函数求出其在(0,1]上的单调性,进而求出其最大值,只须让起最大值与1相比即可求出实数a的取值范围
解:(1)∵ 的图象与
的图象与 的图象关于y轴对称,
的图象关于y轴对称,
∴ 的图象上任意一点
的图象上任意一点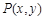 关于
关于 轴对称的对称点
轴对称的对称点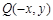 在
在 的图象上.
的图象上.
当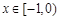 时,
时, ,则
,则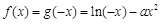 . 2分
. 2分
∵ 为
为 上的奇函数,则
上的奇函数,则 . 3分
. 3分
当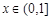 时,
时,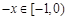 ,
,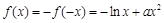 . 5分
. 5分
∴ 6分
6分
(2)由已知,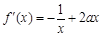 .
.
①若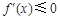 在
在 恒成立,则
恒成立,则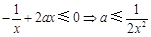 .
.
此时, ,
, 在
在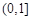 上单调递减,
上单调递减,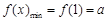 ,
,
∴ 的值域为
的值域为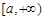 与
与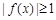 矛盾. 8分
矛盾. 8分
②当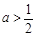 时,令
时,令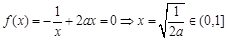 ,
,
∴当 时,
时,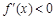 ,
, 单调递减,
单调递减,
当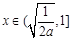 时,
时, ,
, 单调递增,
单调递增,
∴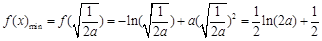 . 10分
. 10分
由 ,得
,得 .
.
综上所述,实数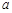 的取值范围为
的取值范围为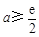 . 12分
. 12分
(1)先利用函数g(x)与f(x)的图象关于y轴对称得:f(x)的图象上任意一点P(x,y)关于y轴对称的对称点Q(-x,y)在g(x)的图象上;然后再利用x∈[-1,0)时,-x∈(0,1],则f(x)=g(-x)求出一段解析式,再利用定义域内有0,可得f(0)=0;最后利用其为奇函数可求x∈(0,1]时对应的解析式,综合即可求函数f(x)的解析式;
(2)先求出f(x)在(0,1]上的导函数,利用其导函数求出其在(0,1]上的单调性,进而求出其最大值,只须让起最大值与1相比即可求出实数a的取值范围
解:(1)∵
 的图象与
的图象与 的图象关于y轴对称,
的图象关于y轴对称,∴
 的图象上任意一点
的图象上任意一点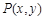 关于
关于 轴对称的对称点
轴对称的对称点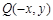 在
在 的图象上.
的图象上.当
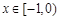 时,
时, ,则
,则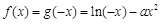 . 2分
. 2分∵
 为
为 上的奇函数,则
上的奇函数,则 . 3分
. 3分当
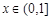 时,
时,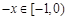 ,
,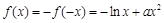 . 5分
. 5分∴
 6分
6分(2)由已知,
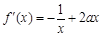 .
.①若
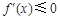 在
在 恒成立,则
恒成立,则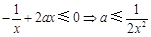 .
.此时,
 ,
, 在
在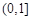 上单调递减,
上单调递减,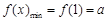 ,
,∴
 的值域为
的值域为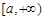 与
与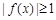 矛盾. 8分
矛盾. 8分②当
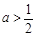 时,令
时,令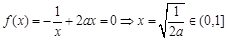 ,
,∴当
 时,
时,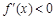 ,
, 单调递减,
单调递减,当
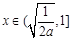 时,
时, ,
, 单调递增,
单调递增,∴
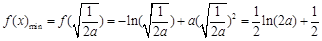 . 10分
. 10分由
 ,得
,得 .
.综上所述,实数
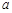 的取值范围为
的取值范围为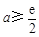 . 12分
. 12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
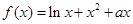 。
。 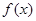 在
在 处取得极值,求
处取得极值,求 的值;
的值;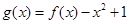 ,当
,当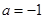 时,
时, 在其定义域内恒成立;
在其定义域内恒成立; 。
。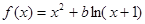 ,其中
,其中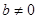
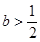 时,判断函数
时,判断函数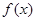 在定义域上的单调性;
在定义域上的单调性;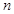 ,不等式
,不等式 都成立。
都成立。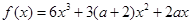 .
.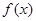 的两个极值点为
的两个极值点为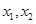 ,且
,且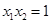 ,求实数
,求实数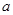 的值;
的值;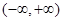 上的单调函数?若存在,求出
上的单调函数?若存在,求出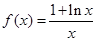 。
。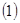 如果
如果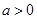 ,函数在区间
,函数在区间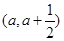 上存在极值,求实数a的取值范围;
上存在极值,求实数a的取值范围;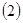 当
当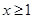 时,不等式
时,不等式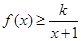 恒成立,求实数k的取值范围。
恒成立,求实数k的取值范围。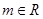 ,函数
,函数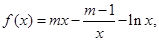
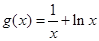 .
.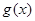 的极值;
的极值;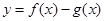 在
在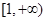 上为单调递增函数,求
上为单调递增函数,求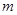 的取值范围;
的取值范围;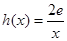 ,若在
,若在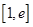 (
(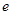 是自然对数的底数)上至少存在一个
是自然对数的底数)上至少存在一个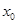 ,使得
,使得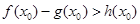 成立,求
成立,求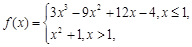 若
若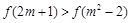 ,则实数
,则实数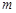 的取值范围是 .
的取值范围是 . 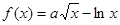
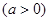
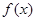 在
在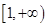 上递增,求
上递增,求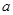 的取值范围;
的取值范围;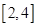 上的存在单调递减区间 ,求
上的存在单调递减区间 ,求