题目内容
设函数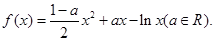 (Ⅰ) 当
(Ⅰ) 当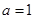 时,求函数
时,求函数 的极值;
的极值;
(Ⅱ)当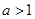 时,讨论函数
时,讨论函数 的单调性. (Ⅲ)(理科)若对任意
的单调性. (Ⅲ)(理科)若对任意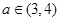 及任意
及任意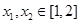 ,恒有
,恒有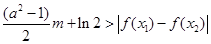 成立,求实数
成立,求实数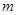 的取值范围.
的取值范围.
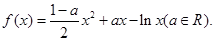 (Ⅰ) 当
(Ⅰ) 当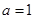 时,求函数
时,求函数 的极值;
的极值;(Ⅱ)当
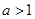 时,讨论函数
时,讨论函数 的单调性. (Ⅲ)(理科)若对任意
的单调性. (Ⅲ)(理科)若对任意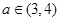 及任意
及任意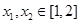 ,恒有
,恒有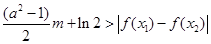 成立,求实数
成立,求实数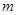 的取值范围.
的取值范围.(Ⅰ) 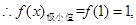 无极大值.
无极大值.
(Ⅱ)当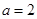 时,
时, 在
在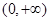 上是减函数;
上是减函数;
当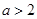 时,
时, 在
在 和
和 单调递减,在
单调递减,在 上单调递增;
上单调递增;
当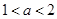 时,
时, 在
在 和
和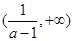 单调递减,在
单调递减,在 上单调递增;
上单调递增;
(Ⅲ)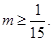 。
。
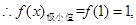 无极大值.
无极大值.(Ⅱ)当
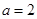 时,
时, 在
在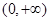 上是减函数;
上是减函数;当
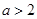 时,
时, 在
在 和
和 单调递减,在
单调递减,在 上单调递增;
上单调递增;当
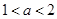 时,
时, 在
在 和
和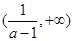 单调递减,在
单调递减,在 上单调递增;
上单调递增; (Ⅲ)
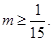 。
。(I)当a=1时,直接求导,利用导数大(小)于零,分别求出其单调增(减)区间.
(II)当a>1时,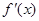
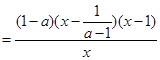 ,然后
,然后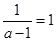 和
和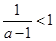 和
和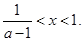 ,三种情况讨论其单调性.
,三种情况讨论其单调性.
(III)由(Ⅱ)知,当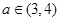 时,
时, 在
在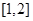 上单减,
上单减, 是最大值,
是最大值,  是最小值.
是最小值.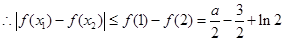 ,从而得到
,从而得到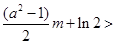
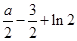 ,然后分离参数m,转化为不等式恒成立来解决.
,然后分离参数m,转化为不等式恒成立来解决.
请考生在22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分.
(Ⅰ)函数的定义域为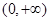 .
.
当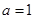 时,
时,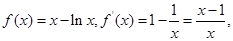
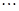 2分
2分
当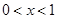 时,
时,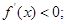 当
当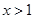 时,
时,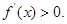
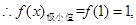 无极大值.
无极大值.  4分
4分
(Ⅱ)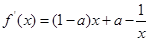

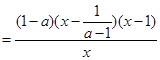
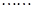 5分
5分
当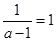 ,即
,即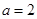 时,
时,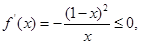
 在定义域上是减函数;
在定义域上是减函数;
当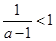 ,即
,即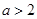 时,令
时,令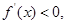 得
得 或
或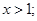 令
令 得
得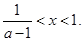 当
当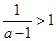 ,即
,即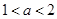 时,令
时,令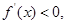 得
得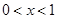 或
或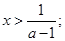
令 得
得 综上,当
综上,当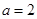 时,
时, 在
在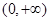 上是减函数;
上是减函数;
当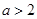 时,
时, 在
在 和
和 单调递减,在
单调递减,在 上单调递增;
上单调递增;
当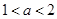 时,
时, 在
在 和
和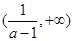 单调递减,在
单调递减,在 上单调递增;
上单调递增;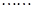 8分
8分
(Ⅲ)由(Ⅱ)知,当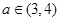 时,
时, 在
在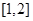 上单减,
上单减, 是最大值,
是最大值,  是最小值.
是最小值.
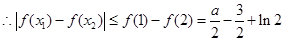 , 10分
, 10分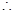
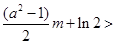
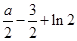
而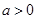 经整理得
经整理得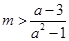 ,由
,由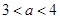 得
得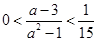 ,所以
,所以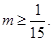
 12分
12分
(II)当a>1时,
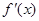
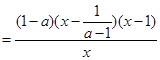 ,然后
,然后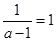 和
和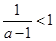 和
和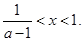 ,三种情况讨论其单调性.
,三种情况讨论其单调性.(III)由(Ⅱ)知,当
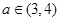 时,
时, 在
在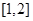 上单减,
上单减, 是最大值,
是最大值,  是最小值.
是最小值.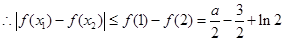 ,从而得到
,从而得到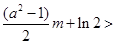
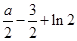 ,然后分离参数m,转化为不等式恒成立来解决.
,然后分离参数m,转化为不等式恒成立来解决.请考生在22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分.
(Ⅰ)函数的定义域为
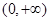 .
. 当
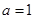 时,
时,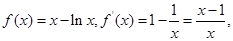
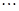 2分
2分当
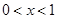 时,
时,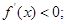 当
当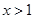 时,
时,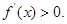
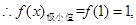 无极大值.
无极大值. 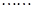 4分
4分(Ⅱ)
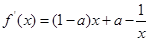

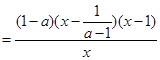
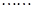 5分
5分当
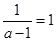 ,即
,即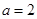 时,
时,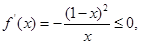
 在定义域上是减函数;
在定义域上是减函数;当
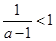 ,即
,即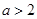 时,令
时,令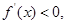 得
得 或
或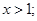 令
令 得
得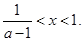 当
当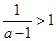 ,即
,即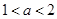 时,令
时,令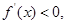 得
得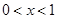 或
或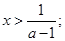
令
 得
得 综上,当
综上,当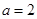 时,
时, 在
在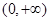 上是减函数;
上是减函数;当
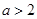 时,
时, 在
在 和
和 单调递减,在
单调递减,在 上单调递增;
上单调递增;当
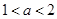 时,
时, 在
在 和
和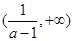 单调递减,在
单调递减,在 上单调递增;
上单调递增;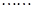 8分
8分(Ⅲ)由(Ⅱ)知,当
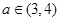 时,
时, 在
在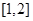 上单减,
上单减, 是最大值,
是最大值,  是最小值.
是最小值.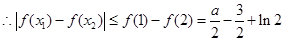 , 10分
, 10分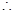
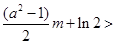
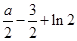
而
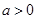 经整理得
经整理得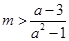 ,由
,由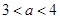 得
得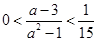 ,所以
,所以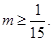
 12分
12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
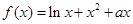 。
。 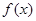 在
在 处取得极值,求
处取得极值,求 的值;
的值;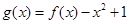 ,当
,当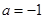 时,
时, 在其定义域内恒成立;
在其定义域内恒成立; 。
。 .
. 时,如果函数
时,如果函数 仅有一个零点,求实数
仅有一个零点,求实数 的取值范围;
的取值范围; 时,试比较
时,试比较 与1的大小;
与1的大小;
 .
.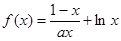 .
. 在
在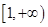 上是增函数,求正实数
上是增函数,求正实数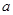 的取值范围;
的取值范围;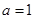 时,求函数
时,求函数 上的最大值和最小值;
上的最大值和最小值; 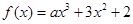 ,若
,若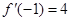 ,则
,则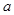 的值等于( )
的值等于( )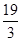


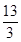
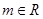 ,函数
,函数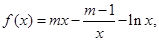
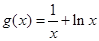 .
.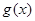 的极值;
的极值;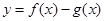 在
在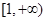 上为单调递增函数,求
上为单调递增函数,求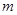 的取值范围;
的取值范围;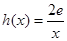 ,若在
,若在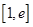 (
(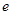 是自然对数的底数)上至少存在一个
是自然对数的底数)上至少存在一个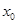 ,使得
,使得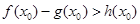 成立,求
成立,求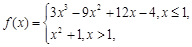 若
若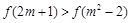 ,则实数
,则实数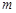 的取值范围是 .
的取值范围是 . 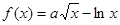
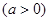
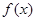 在
在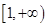 上递增,求
上递增,求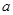 的取值范围;
的取值范围;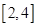 上的存在单调递减区间 ,求
上的存在单调递减区间 ,求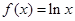 ,
,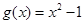 ,
,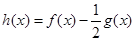 的最值;
的最值;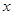 ,恒有
,恒有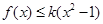 成立,求实数
成立,求实数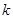 的取值组成的集合。
的取值组成的集合。