题目内容
【题目】已知函数
在
处取得极值，且在
处的切线的斜率为-3.（Ⅰ）求
的解析式；
（Ⅱ）若过点A（2，
）可作曲线
的三条切线，求实数的取值范围.
【答案】（1）
（2）（－6，2）
【解析】分析：(I)由函数
在
处取得极值，且在
处的切线的斜率为-3，求导，可得
是
的两根，且
，解方程组即可求得
的值，从而求得
的解析式；（II）设切点，求切线方程，得到
，要求过点A（2，
）可作曲线
的三条切线，即求，有三个零点，画出函数的草图，即可求得实数的取值范围.
详解：（Ⅰ）
依题意
又
∴ 
∴
∴（Ⅰ）
（Ⅱ）设切点为（
）， ∵
∴
∴ 切线方程为
又切线过点A（2，） ∴ 
∴
令
则 
由
得或
，
画出草图知，当
＜＜
时，
有三解，
所以的取值范围是（－6，2）.
【题目】已知双曲线 
与双曲线 
的离心率相同，且双曲线C2的左、右焦点分别为F1 ， F2 ， M是双曲线C2一条渐近线上的某一点，且OM⊥MF2 ， 
，则双曲线C2的实轴长为（ ）
A.4
B.
C.8
D.
【题目】某种产品的质量以其质量指标值衡量，并依据质量指标值划分等极如下表：
质量指标值m | m＜185 | 185≤m＜205 | m≥205 |
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件，检测后得到如下的频率分布直方图：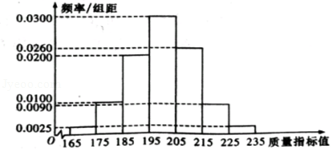
（Ⅰ）根据以上抽样调查数据，能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品90%”的规定？
（Ⅱ）在样本中，按产品等极用分层抽样的方法抽取8件，再从这8件产品中随机抽取4件，求抽取的4件产品中，一、二、三等品都有的概率；
（III）该企业为提高产品质量，开展了“质量提升月”活动，活动后再抽样检测，产品质量指标值X近似满足X～N（218，140}），则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少？
