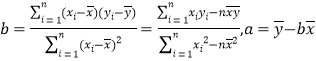题目内容
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等极如下表:
质量指标值m | m<185 | 185≤m<205 | m≥205 |
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图: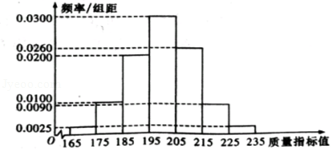
(Ⅰ)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品90%”的规定?
(Ⅱ)在样本中,按产品等极用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(III)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值X近似满足X~N(218,140}),则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
【答案】解:(Ⅰ)根据抽样调查数据,一、二等品所占比例的估计值为0.200+0.300+0.260+0.090+0.025=0.875, 由于该估计值小于0.90,
故不能认为该企业生产的这种产品符合“一、二等品至少要占全部产品90%”的规定.
(Ⅱ)由频率分布直方图知,一、二、三等品的频率分别为0.375、0.5、0.125,
故在样本中用分层抽样方法抽取的8件产品中,一等品3件,二等品4件,三等品1件,
再从这8件产品中随机抽取4件,一、二、三等品都有的情况有2种:
①一等品2件,二等品1件,三等品1件;②一等品1件,二等品2件,三等品1件,
故所求的概率 ![]() .
.
(Ⅲ)“质量提升月”活动前,该企业这种产品的质量指标值的均值约为:
170×0.025+180×0.1+190×0.2+200×0.3+210×0.26+220×0.09+230×0.025=200.4
“质量提升月”活动后,产品质量指标值X近似满足X~N(218,140),则E(X)=218.
所以,“质量提升月”活动后的质量指标值的均值比活动前大约提升了:218﹣200.4=17.6
【解析】(Ⅰ)根据抽样调查数据,一、二等品所占比例的估计值为0.875,由于该估计值小于0.90,由此不能认为该企业生产的这种产品符合“一、二等品至少要占全部产品90%”的规定.(Ⅱ)由频率分布直方图知,一、二、三等品的频率分别为0.375、0.5、0.125,在样本中用分层抽样方法抽取的8件产品中,一等品3件,二等品4件,三等品1件,再从这8件产品中随机抽取4件,一、二、三等品都有的情况有2种:①一等品2件,二等品1件,三等品1件;②一等品1件,二等品2件,三等品1件,由此能求出抽取的4件产品中,一、二、三等品都有的概率.(Ⅲ)“质量提升月”活动前,该企业这种产品的质量指标值的均值约为200.4“质量提升月”活动后,产品质量指标值X近似满足X~N(218,140),则E(X)=218.由此能求出“质量提升月”活动后的质量指标值的均值比活动前大约提升了17.6.
【考点精析】解答此题的关键在于理解频率分布直方图的相关知识,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.

 星级口算天天练系列答案
星级口算天天练系列答案【题目】某校600名文科学生参加了4月25日的三调考试,学校为了了解高三文科学生的数学、外语情况,利用随机数表法从抽取100名学生的成绩进行统计分析,将学生编号为000,001,002,…599
12 56 85 99 26 96 96 68 27 31 05 03 72 93 15 57 12 10 14 21 88 26 49 81 76
55 59 56 35 64 38 54 82 46 22 31 62 43 09 90 06 18 44 32 53 23 83 01 30 30
16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
(1)若从第6行第7列的数开始右读,请你一次写出最先抽出的5个人的编号(上面是摘自随机数表的第4行到第7行);
(2)抽出的100名学生的数学、外语成绩如下表:
外语 | ||||
优 | 良 | 及格 | ||
数学 | 优 | 8 | m | 9 |
良 | 9 | n | 11 | |
及格 | 8 | 9 | 11 | |
若数学成绩优秀率为35%,求m,n的值;
(3)在外语成绩为良的学生中,已知m≥12,n≥10,求数学成绩优比良的人数少的概率.
【题目】某研究机构对春节燃放烟花爆竹的天数x与雾霾天数y进行统计分析,得出下表数据.
x | 4 | 5 | 7 | 8 |
y | 2 | 3 | 5 | 6 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(2)试根据(1)求出的线性回归方程,预测燃放烟花爆竹的天数为9的雾霾天数.
相关公式: