题目内容
【题目】已知双曲线 ![]() 与双曲线
与双曲线 ![]() 的离心率相同,且双曲线C2的左、右焦点分别为F1 , F2 , M是双曲线C2一条渐近线上的某一点,且OM⊥MF2 ,
的离心率相同,且双曲线C2的左、右焦点分别为F1 , F2 , M是双曲线C2一条渐近线上的某一点,且OM⊥MF2 , ![]() ,则双曲线C2的实轴长为( )
,则双曲线C2的实轴长为( )
A.4
B.![]()
C.8
D.![]()
【答案】D
【解析】解:双曲线 ![]() 中,a1=
中,a1= ![]() ,c1=
,c1= ![]() =2
=2 ![]() ,则离心率e=
,则离心率e= ![]() =
= ![]() =
= ![]() , 即c=
, 即c= ![]() a,则b2=c2﹣a2=
a,则b2=c2﹣a2= ![]() a2 , 得b=
a2 , 得b= ![]() a,即
a,即 ![]() =
= ![]() ,
,
设双曲线的渐近线为y= ![]() x,即bx﹣ay=0,
x,即bx﹣ay=0,
则右焦点F2 ,
∵OM⊥MF2 ,
∴MF2= ![]() =
= ![]() ,
,
则渐近线y= ![]() x=
x= ![]() x,则渐近线的倾斜角∠MOF2=30°,∠OF2M=60°,
x,则渐近线的倾斜角∠MOF2=30°,∠OF2M=60°,
则OF2=2MF2 , 即c=2b,
则三角形的面积 ![]() =
= ![]() OF2MF2sin60°=
OF2MF2sin60°= ![]() ×b2b
×b2b ![]() =
= ![]() b2 ,
b2 ,
则b2=16,则a2=3b2=48,则a=4 ![]() ,
,
则2a= ![]() ,
,
即双曲线C2的实轴长为 ![]() ,
,
故选:D.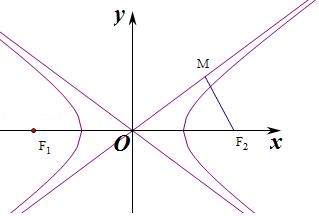

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目