题目内容
【题目】下列命题是真命题的是( )
A. φ∈R,函数f(x)=sin(2x+φ)都不是偶函数
B. α,β∈R,使cos(α+β)=cosα+cosβ
C. 向量a=(2,1),b=(-1,0),则a在b的方向上的投影为2
D. “|x|≤1”是“x≤1”的既不充分又不必要条件
【答案】B
【解析】逐一考查所给的命题:
选项A,当φ=![]() 时,f(x)=cos2x,其为偶函数,故A为假命题;
时,f(x)=cos2x,其为偶函数,故A为假命题;
选项B,令![]() ,则
,则![]() ,
, ![]() ,cos(α+β)=cosα+cosβ成立,故B为真命题;
,cos(α+β)=cosα+cosβ成立,故B为真命题;
选项C,设![]() 与
与![]() 的夹角为θ,
的夹角为θ, 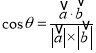 ,则
,则![]() 在
在![]() 的方向上的投影为
的方向上的投影为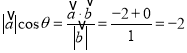 ,故C为假命题;
,故C为假命题;
选项D,|x|≤1,-1≤x≤1,故充分性成立,若x≤1,|x|≤1不一定成立,故为充分不必要条件,D为假命题.
本题选择B选项.

练习册系列答案
相关题目