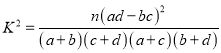题目内容
【题目】公交车的数量太多容易造成资源浪费,太少又难以满足乘客的需求,为了合理布置车辆,公交公司在2路车的乘客中随机调查了50名乘客,经整理,他们候车时间(单位:![]() )的茎叶图如下:
)的茎叶图如下:

(Ⅰ)将候车时间分为![]() 八组,作出相应的频率分布直方图;
八组,作出相应的频率分布直方图;
(Ⅱ)若公交公司将2路车发车时间调整为每隔15![]() 发一趟车,那么上述样本点将发生变化(例如候车时间为9
发一趟车,那么上述样本点将发生变化(例如候车时间为9![]() 的不变,候车时间为17
的不变,候车时间为17![]() 的变为2
的变为2![]() ),现从2路车的乘客中任取5人,设其中候车时间不超过10
),现从2路车的乘客中任取5人,设其中候车时间不超过10![]() 的乘客人数为
的乘客人数为![]() ,求
,求![]() 的数学期望.
的数学期望.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】试题分析:
(Ⅰ)根据茎叶图可得落在各组内的频数,求得频率后可得![]() 的值,根据所得数据可得频率分布直方图.(Ⅱ)由题意得候车时间中不超过10分钟的数据共有34个,根据古典概型概率公式可得所求概率为0.68.
的值,根据所得数据可得频率分布直方图.(Ⅱ)由题意得候车时间中不超过10分钟的数据共有34个,根据古典概型概率公式可得所求概率为0.68.
试题解析:
(Ⅰ)由茎叶图可得落入分组区间![]() 内的频数依次为4、4、10、12、8、6、4、2,
内的频数依次为4、4、10、12、8、6、4、2,
于是可得各组分组区间相应的![]() 的值依次为0.02、0.02、0.05、0.06、0.04、0.03、0.02、
的值依次为0.02、0.02、0.05、0.06、0.04、0.03、0.02、
0.01,
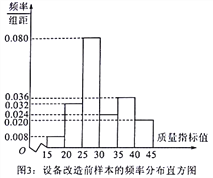
依此画出频率分布直方图如下图所示.
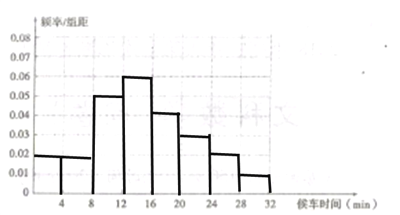
(Ⅱ)调整为间隔15分钟发一趟车之后,候车时间原本不超过10分钟的数据就有14个,发生了变化的候车时间中不超过10分钟的数据又增加了20个,共计34个.
所以候车时间不超过10分钟的频率为![]() ,
,
由此估计一名乘客候车时间不超过10分钟的概率为0.68.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目