题目内容
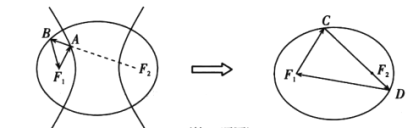
【题目】光线从椭圆的一个焦点发出，被椭圆反射后会经过椭圆的另一个焦点；光线从双曲线的一个焦点发出，被双曲线反射后的反射光线等效于从另一个焦点射出.如图，一个光学装置由有公共焦点
，
的椭圆
与双曲线
构成，现一光线从左焦点发出，依次经与反射，又回到了点，历时
秒；若将装置中的去掉，此光线从点发出，经两次反射后又回到了点，历时
秒；若
，则与的离心率之比为（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
根据椭圆和双曲线的定义，分别列出关系式再做差，得出椭圆双曲线“复合”光学装置中光线路程；然后计算单椭圆光学装置中光线路程，两者相比可得出椭圆长半轴和双曲线实半轴的关系，即可得两离心率的关系.
解：如图，由双曲线定义得：
①，
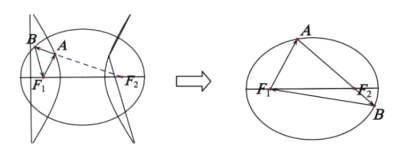
由椭圆定义得：
②，
②-①得：
；
所以椭圆双曲线“复合”光学装置中，光线从出发到回到左焦点走过的路程为
对于单椭圆光学装置，光线经过2次反射后回到左焦点，路程为
；
由于两次光速相同，路程比等于时间比，所以
，所以
.
所以
.
故选：B.
练习册系列答案
相关题目
