题目内容
【题目】某校早上8：00开始上课，假设该校学生小张与小王都在早上7：30--7：50之间到校，且每人在该时间段的任何时刻到校是等可能的，求小张比小王至少早5分钟到校的概率.
【答案】
【解析】
用x表示小张到校的时间则30≤x≤50，用y表示小王到校的时间，则30≤y≤50. 则所有可能的结果对应直角坐标平面内的正方形区域, 记“小张比小王至少早5分钟到校"为事件M.则M所对区域为图中的图影部分,利用几何概型计算可得答案.
解：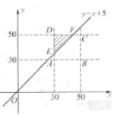
用x表示小张到校的时间则30≤x≤50，用y表示小王到校的时间，则30≤y≤50. 则所有可能的结果对应直角坐标平面内的正方形区域ABCD.
记“小张比小王至少早5分钟到校"为事件M.
则M所对区域为图中的图影部分△DEF.
所以
练习册系列答案
阅读快车系列答案
相关题目
【题目】某校高一、高二年级的全体学生都参加了体质健康测试，测试成绩满分为100分，规定测试成绩在
之间为“体质优秀”，在
之间为“体质良好”，在
之间为“体质合格”，在
之间为“体质不合格”
现从两个年级中各随机抽取8名学生，测试成绩如下：
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
高一年级 | 60 | 85 | 55 | 80 | 65 | 90 | 90 | 75 |
高二年级 | 75 | 85 | 65 | 90 | 75 | 60 | a | b |
其中a，b是正整数．
（1）若该校高一年级有200名学生，试估计高一年级“体质优秀”的学生人数；
（2）从高一年级抽取的学生中再随机选取3人，求这3人中，恰有1人“体质良好”的概率；
（3）设两个年级被抽取学生的测试成绩的平均数相等，当高二年被抽取学生的测试成绩的方差最小时，写出a，b的值
结论不要求证明
