题目内容
【题目】已知二次函数
，满足
，
.
（1）求函数
的解析式；
（2）若关于
的不等式
在
上有解，求实数
的取值范围；
（3）若函数
的两个零点分别在区间
和
内，求实数
的取值范围.
【答案】（1）
（2）
（3）
【解析】
（1）通过
,求出
,利用
,可得出函数的对称轴为
,即可求
,进而得到函数的解析式;
（2）求出函数
的对称轴,然后求解
,列出
关系式,即可求解实数
的取值范围;
（3）将代入
得
,若
的两个零点分别在区间
和
内,利用零点存在定理列出不等式组求解,即可求得实数
的取值范围.
（1）
,得
根据
的对称轴为
可得的对称轴为
是二次函数
根据二次函数的对称轴为
故
得
解析式为: .
（2） 
对称轴为
关于
的不等式
在
有解,
则
所以实数的取值范围是:.
（3
将代入
,得
要保证的两个零点分别在区间和内则保证:
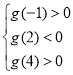化简可得:
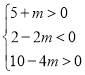解得:
所以实数的取值范围为:
练习册系列答案
相关题目
【题目】某校高一、高二年级的全体学生都参加了体质健康测试，测试成绩满分为100分，规定测试成绩在
之间为“体质优秀”，在
之间为“体质良好”，在
之间为“体质合格”，在
之间为“体质不合格”
现从两个年级中各随机抽取8名学生，测试成绩如下：
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
高一年级 | 60 | 85 | 55 | 80 | 65 | 90 | 90 | 75 |
高二年级 | 75 | 85 | 65 | 90 | 75 | 60 | a | b |
其中a，b是正整数．
（1）若该校高一年级有200名学生，试估计高一年级“体质优秀”的学生人数；
（2）从高一年级抽取的学生中再随机选取3人，求这3人中，恰有1人“体质良好”的概率；
（3）设两个年级被抽取学生的测试成绩的平均数相等，当高二年被抽取学生的测试成绩的方差最小时，写出a，b的值
结论不要求证明
