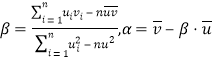题目内容
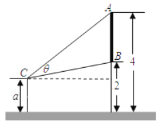
【题目】墙上有一壁画,最高点![]() 处离地面
处离地面![]() 米,最低点
米,最低点![]() 处离地面
处离地面![]() 米,距离墙
米,距离墙![]() 米处设有防护栏,观察者从离地面高
米处设有防护栏,观察者从离地面高![]() 米的
米的![]() 处观赏它.
处观赏它.
(1)当![]() 时,观察者离墙多远时,视角
时,观察者离墙多远时,视角![]() 最大?
最大?
(2)若![]() ,视角
,视角![]() 的正切值恒为
的正切值恒为![]() ,观察者离墙的距离应在什么范围内?
,观察者离墙的距离应在什么范围内?
【答案】(1)当观察者离墙![]() 米处时,视角
米处时,视角![]() 最大;(2)
最大;(2)![]() .
.
【解析】
(1)过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,设观察者离墙
,设观察者离墙![]() 米,则
米,则![]() ,求出
,求出![]() 和
和![]() ,利用两角差的正切公式可得出
,利用两角差的正切公式可得出![]() 关于
关于![]() 的表达式,利用基本不等式可求得
的表达式,利用基本不等式可求得![]() 的最大值,进而得解;
的最大值,进而得解;
(2)求得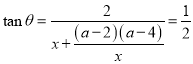 ,可得出
,可得出![]() ,由
,由![]() 可得出
可得出![]() ,结合
,结合![]() 可得出
可得出![]() 的取值范围,进而得解.
的取值范围,进而得解.
(1)当![]() 时,过
时,过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,则
,则![]() ,且
,且![]() ,
,
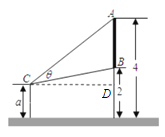
设观察者离墙![]() 米,则
米,则![]() ,且
,且![]() ,
,![]() ,
,
所以,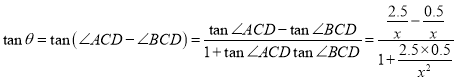
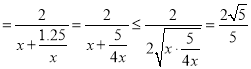 ,
,
当且仅当![]() ,即当
,即当![]() 时,
时,![]() 取最大值
取最大值![]() ,此时视角
,此时视角![]() 最大;
最大;
(2)由(1)得![]() ,
,![]() ,
,
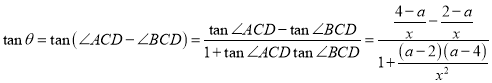
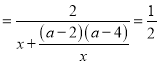 ,
,
即![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,解得
,解得![]() 或
或![]() .
.
![]() ,所以,
,所以,![]() .
.
因此,观察者离墙的距离应在![]() 至
至![]() 米范围内.
米范围内.

【题目】
某初级中学共有学生2000名,各年级男、女生人数如下表:
初一年级 | 初二年级 | 初三年级 | |
女生 | 373 | x | y |
男生 | 377 | 370 | z |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
求x的值;
现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
已知y![]() 245,z
245,z![]() 245,求初三年级中女生比男生多的概率.
245,求初三年级中女生比男生多的概率.
【题目】某公司为了确定下一年度投入某种产品的宣传费用,需了解年宣传费x(单位:万元)对年销量y(单位:吨)和年利润(单位:万元)的影响.对近6宣传费xi和年销售量yi(i=1,2,3,4,5,6)的数据做了初步统计,得到如下数据:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年宣传费x(万元) | 38 | 48 | 58 | 68 | 78 | 88 |
年销售量y(吨) | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
经电脑模拟,发现年宣传费x(万元)与年销售量y(吨)之间近似满足关系式y=axb(a,b>0),即lny=blnx+lna.,对上述数据作了初步处理,得到相关的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(Ⅰ)从表中所给出的6年年销售量数据中任选2年做年销售量的调研,求所选数据中至多有一年年销售量低于20吨的概率.
(Ⅱ)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅲ) 若生产该产品的固定成本为200(万元),且每生产1(吨)产品的生产成本为20(万元)(总成本=固定成本+生产成本+年宣传费),销售收入为![]() (万元),假定该产品产销平衡(即生产的产品都能卖掉),则2019年该公司应该投入多少宣传费才能使利润最大?(其中
(万元),假定该产品产销平衡(即生产的产品都能卖掉),则2019年该公司应该投入多少宣传费才能使利润最大?(其中![]() )
)
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为