Question

【题目】已知椭圆的离心率为，且过点．

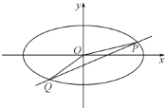
（Ⅰ）求椭圆方程；

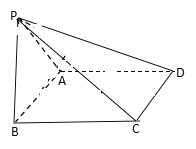
（Ⅱ）设不过原点的直线，与该椭圆交于两点，直线的斜率分别为，满足．

（i）当变化时，是否为定值？若是，求出此定值，并证明你的结论；若不是，请说明理由；

（ii）求面积的取值范围．

Answer 1

【答案】（Ⅰ）y2＝1；（Ⅱ）（i）见解析；（ii）（0，1）.

【解析】

（Ⅰ）由题设条件，设ck，a＝2k，则b＝k，利用待定系数法能求出椭圆方程．

（Ⅱ）（i）由，得（1+4k2）x2+8kmx+4（m2﹣1）＝0，由此利用根的判别式、韦达定理、斜率性质，结合已知条件推导出当k变化时，m2是定值．

②利用椭圆弦长公式，结合已知条件能求出△OPQ面积的取值范围．

（Ⅰ）由题设条件，设ck，a＝2k，则b＝k，

∴椭圆方程为1，

把点（，）代入，得k2＝1，

∴椭圆方程为y2＝1．

（Ⅱ）（i）当k变化时，m2是定值．

证明如下：

由，得（1+4k2）x2+8kmx+4（m2﹣1）＝0，设

∴，．

∵直线OP，OQ的斜率依次为k1，k2，

∴4k＝k1+k2，

∴2kx1x2＝m（x1+x2），由此解得，验证△＞0成立．

∴当k变化时，是定值．

②S△OPQ|x1﹣x2||m|，令t＞1，

得S△OPQ1，

∴△OPQ面积的取值范围S△OPQ∈（0，1）．