题目内容
【题目】已知椭圆
的中心在原点，焦点在
轴，离心率为
，且长轴长是短轴长的
倍.
（1）求椭圆
的标准方程；
（2）设
过椭圆
左焦点
的直线
交
于
， 
两点，若对满足条件的任意直线
，不等式
恒成立，求
的最小值.
【答案】（1）
（2）
【解析】试题分析：（1）采用待定系数法，根据条件所给的几何关系列式，再结合
，解出
；（2）首先分两种情况，当直线与
轴垂直的时候，可得出
两点的坐标，从而计算可得
的值，当直线与
轴不垂直的时候，设直线
与椭圆方程联立，得到根与系数的关系，带入
的坐标关系,得到函数的最大值，比较两种情况下的最大值， 
，从而得出
的最小值.
试题解析：（1）依题意，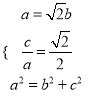 
，
解得
， 
， 
椭圆
的标准方程为
.
（2）设
， 
，
当直线
垂直于
轴时， 
， 
且
，
此时
， 
， 
.
当直线
不垂直于
轴时，设直线
： 
，
由
，得
，
， 
，
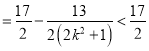
要使不等式
恒成立，
只需
，即
的最小值为
.
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
【题目】某连锁经营公司所属5个零售店某月的销售额和利润额如下表：
商店名称 | A | B | C | D | E |
销售额x/千万元 | 3 | 5 | 6 | 7 | 9 |
利润额y/百万元 | 2 | 3 | 3 | 4 | 5 |
（1）画出散点图，观察散点图，说明两个变量是否线性相关；
（2）用最小二乘法计算利润额y对销售额x的线性回归方程；
（3）当销售额为4千万元时，估计利润额的大小.
（参考公式：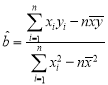
，
）
