题目内容
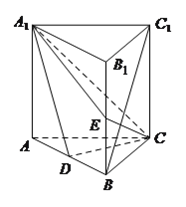
【题目】如图所示,在四棱台ABCD﹣A1B1C1D1中,底面ABCD是平行四边形,DD1⊥平面ABCD,AB=2AD,AD=A1B1,∠BAD=60°.
(Ⅰ)证明:CC1∥平面A1BD;
(Ⅱ)求直线CC1与平面ADD1A1所成角的正弦值

【答案】(1)见解析(2) ![]()
【解析】【试题分析】(1)连接![]() 、
、![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,利用
,利用![]() 证得四边形
证得四边形![]() 是平行四边形,故
是平行四边形,故![]() ,所以
,所以![]() 平面
平面![]() .(2)由于BD⊥平面ADD1A1得,
.(2)由于BD⊥平面ADD1A1得, ![]() 就是所求直线与平面所成的角.解三角形可求得其正弦值.
就是所求直线与平面所成的角.解三角形可求得其正弦值.
【试题解析】
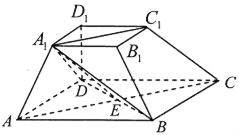 (1)证明:连接AC,A1C1,设AC∩BD=E,连接EA1,
(1)证明:连接AC,A1C1,设AC∩BD=E,连接EA1,
∵四边形ABCD是平行四边形,
∴EC=![]() AC,
AC,
由棱台定义及AB=2AD=2A1B1知
A1C1∥EC,且A1C1=EC,
∴四边形A1ECC1是平行四边形,因此CC1∥EA1,
又∵EA1平面A1BD,
∴CC1∥平面A1BD;
(2)解:直线EA1与平面ADD1A1所成角=直线CC1与平面ADD1A1所成角,
∵BD⊥平面ADD1A1,∴A1D为EA1在平面ADD1A1上的射影,
∴∠EA1D是直线EA1与平面ADD1A1所成角,
∵DD1=AD,AB=2AD,AD=A1B1M∠BAD=60°,
∴A1D1=![]() AD,DE=
AD,DE=![]() AD,A1E=
AD,A1E=![]() AD,
AD,
∴sin∠EA1D=![]() ,
,
∴直线CC1与平面ADD1A1所成角的正弦值为![]() .
.

练习册系列答案
相关题目