Question

【题目】已知函数

(1)若函数在区间[0,1]上存在零点，求实数的取值范围；

(2)当时，若对任意∈[0,4]，总存在∈[0,4]，使成立，求实数的取值范围．

Answer 1

【答案】(1) [－,1]． (2) m≥2或 m≤－2.

【解析】

（1）由题意，函数，得到其对称轴为，要使得函数在有零点，则满足且，即可求解；

（2）当时，分别求得函数的值域，得到集合，再由题意对于任意∈[0,4]，总存在∈[0,4]，使成立，转化为，根据集合的运算即可求解.

(1)

∵f(x)＝x2－4x＋2a＋1＝(x－2)2＋，

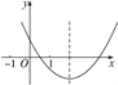
∴函数f(x)图象的对称轴为直线x＝2，要使f(x)在[0,1]上

有零点，其图象如图，则即∴－≤a≤1.

所以所求实数a的取值范围是[－,1]．

(2)当a＝1时，f(x)＝x2－4x＋3＝(x－2)2－1.

∴当x∈[0,4]时，f(x)∈[－1,3]，记A＝[－1,3]．

由题意知

当m=0时g(x)=3显然不适合题意..

当m＞0时，g(x)＝mx＋3－2m在[0,4]上是增函数，∴g(x)∈[3－2m, 2m+3]，记B＝[3－2m, 2m+3]，由题意，知AB.

∴解得m≥2.

当m＜0时，g(x)＝mx＋3－2m在[0,4]上是减函数，∴g(x)∈[2m+3,3－2m]，记C＝ [2m+3,3－2m]，

由题意，知AC.∴解得m≤－2.

综上所述:m≥2或 m≤－2.