题目内容
【题目】函数f(x)=aln x+bx2图象上点P(1,f(1))处的切线方程为2x-y-3=0.
(1)求函数f(x)的解析式及单调区间;
(2)若函数g(x)=f(x)+m-ln 4在![]() 上恰有两个零点,求实数m的取值范围.
上恰有两个零点,求实数m的取值范围.
【答案】(1)f′(x)=![]() +2bx,f(x)的单调递增区间为(0,
+2bx,f(x)的单调递增区间为(0, ![]() ),单调递减区间为(
),单调递减区间为(![]() ,+∞).(2)2<m≤4-2ln 2.
,+∞).(2)2<m≤4-2ln 2.
【解析】试题分析:(1)由导数的几何意义知切线的斜率为点P处导数,点P也在切线上,构造方程组可得函数![]() 的解析式,再由函数的解析式进行求导,判断导数大于零和小于零的区间,即函数的单调区间;(2)易知函数
的解析式,再由函数的解析式进行求导,判断导数大于零和小于零的区间,即函数的单调区间;(2)易知函数![]() ,令
,令![]() ,分离变量
,分离变量![]() ,构造新的函数
,构造新的函数![]() ,对新函数求导判断函数的单调性,再求出新函数的端点值和极值,从而可得实数m的取值范围.
,对新函数求导判断函数的单调性,再求出新函数的端点值和极值,从而可得实数m的取值范围.
试题解析:∵切点![]() 在直线2x-y-3=0上,∴f(1)=-1.
在直线2x-y-3=0上,∴f(1)=-1.
![]() ,由已知得
,由已知得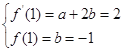
![]() a=4,b=-1.
a=4,b=-1.
∴![]() .
.
∴单调增区间为(0,![]() ),减区间为[
),减区间为[![]() ,+
,+![]()
(2)f(x)的定义域为![]() .
. ![]() =4lnx-x2+m-ln4.
=4lnx-x2+m-ln4.
令g(x)="0," 得4lnx-x2+m-ln4.=0![]() m=x2-4lnx+ln4.
m=x2-4lnx+ln4.
记![]() .则
.则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
![]() ,
,![]()
![]() .
.
由题意,![]() .
.

练习册系列答案
相关题目





