题目内容
【题目】已知函数![]() ,其中
,其中![]() 为正实数.
为正实数.
(1)若函数![]() 在
在![]() 处的切线斜率为2,求
处的切线斜率为2,求![]() 的值;
的值;
(2)求函数![]() 的单调区间;
的单调区间;
(3)若函数![]() 有两个极值点
有两个极值点![]() ,求证:
,求证: ![]() .
.
【答案】(1)1(2) 单调减区间为![]() ,
,![]() ,单调减区间为
,单调减区间为![]() .(3)见解析
.(3)见解析
【解析】试题分析:(1)根据导数几何意义得![]() ,解得
,解得![]() 的值;(2)先求导数,再根据导函数是否变号分类讨论,最后根据导函数符号确定单调区间(3)先根据韦达定理得
的值;(2)先求导数,再根据导函数是否变号分类讨论,最后根据导函数符号确定单调区间(3)先根据韦达定理得![]() ,再化简
,再化简![]() ,进而化简所证不等式为
,进而化简所证不等式为![]() ,最后利用导函数求函数
,最后利用导函数求函数![]() 单调性,进而确定最小值,证得结论
单调性,进而确定最小值,证得结论
试题解析:(1)因为![]() ,所以
,所以![]() ,
,
则![]() ,所以
,所以![]() 的值为1.
的值为1.
(2) ![]() ,函数
,函数![]() 的定义域为
的定义域为![]() ,
,
![]() 若
若![]() ,即
,即![]() ,则
,则![]() ,此时
,此时![]() 的单调减区间为
的单调减区间为![]() ;
;
![]() 若
若![]() ,即
,即![]() ,则
,则![]() 的两根为
的两根为![]() ,
,
此时![]() 的单调减区间为
的单调减区间为![]() ,
,![]() ,
,
单调减区间为![]() .
.
(3)由(2)知,当![]() 时,函数
时,函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]() .
.
因为![]()
![]()
![]()
要证![]() ,只需证
,只需证![]() .
.
构造函数![]() ,则
,则![]() ,
,
![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,且
,且![]() 在定义域上不间断,
在定义域上不间断,
由零点存在定理,可知![]() 在
在![]() 上唯一实根
上唯一实根![]() , 且
, 且![]() .
.
则![]() 在
在![]() 上递减,
上递减, ![]() 上递增,所以
上递增,所以![]() 的最小值为
的最小值为![]() .
.
因为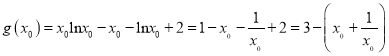 ,
,
当![]() 时,
时, ![]() ,则
,则![]() ,所以
,所以![]() 恒成立.
恒成立.
所以![]() ,所以
,所以![]() ,得证.
,得证.

练习册系列答案
相关题目
【题目】(题文)从某校高一年级随机抽取![]() 名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
组号 | 分组 | 频数 | 频率 |
|
|
|
|
|
|
| |
|
|
| |
|
|
| |
|
|
|

(Ⅰ)求![]() 的值.
的值.
(Ⅱ)若![]() ,补全表中数据,并绘制频率分布直方图.
,补全表中数据,并绘制频率分布直方图.
(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替,若上述数据的平均值为![]() ,求
,求![]() ,
,![]() 的值,并由此估计该校高一学生的日平均睡眠时间不少于
的值,并由此估计该校高一学生的日平均睡眠时间不少于![]() 小时的概率.
小时的概率.


