题目内容
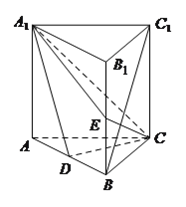
【题目】如图,直三棱柱![]() 中,
中, ![]() 、
、![]() 分别是
分别是![]() ,
, ![]() 的中点,已知
的中点,已知![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
, ![]() .
.
(1)证明: ![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:(1)连接![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() 为
为![]() 的中点,结合
的中点,结合![]() 是
是![]() 的中点,根据三角形中位线定理可得
的中点,根据三角形中位线定理可得![]() ∥
∥![]() ,利用直线与平面平行的判定定理证明
,利用直线与平面平行的判定定理证明![]() 平面
平面![]() ;(2)根据勾股定理可得
;(2)根据勾股定理可得![]() ,以
,以![]() 为坐标原点,
为坐标原点, ![]() 、
、![]() 、
、![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立如图的空间坐标系
轴建立如图的空间坐标系![]() ,利用向量垂直数量积为零,列方程组分别求出平面
,利用向量垂直数量积为零,列方程组分别求出平面![]() 的法向量与平面
的法向量与平面![]() 的法向量,利用空间向量夹角余弦公式可得结果.
的法向量,利用空间向量夹角余弦公式可得结果.
试题解析:(1)证明:连接![]() ,交
,交![]() 于点
于点![]()
则![]() 为
为![]() 的中点
的中点
又![]() 是
是![]() 的中点,连接
的中点,连接![]()
则![]() ∥
∥![]() ,
,
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
所以![]() ∥平面
∥平面![]()
(2)解:易知![]()
则![]() ,得
,得![]()
以![]() 为坐标原点,
为坐标原点, ![]() 、
、![]() 、
、![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立如图的空间坐标系
轴建立如图的空间坐标系![]() ,
,
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]()
设![]() 是平面
是平面![]() 的法向量,
的法向量,
则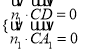 ,即
,即![]() ,
,
可取![]()
同理,设![]() 是平面
是平面![]() 的法向量,则
的法向量,则 ,
,
可取![]()
从而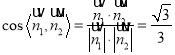
故![]()
即二面角![]() 的正弦值为
的正弦值为![]() .
.

【方法点晴】本题主要考查线面平行的判定定理以及利用空间向量求二面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案【题目】某单位N名员工参加“社区低碳你我他”活动,他们的年龄在25岁至50岁之间。按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,由统计的数据得到的频率分布直方图如图所示,下表是年龄的频率分布表。
,由统计的数据得到的频率分布直方图如图所示,下表是年龄的频率分布表。

区间 |
|
|
|
|
|
人数 |
| a | b |
(1)求正整数a,b,N的值;
(2)现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组中抽取的人数分别是多少?
(3)在(2)的条件下,从这6人中随机抽取2人参加社区宣传交流活动,求恰有1 人在第3组的概率。

