题目内容
【题目】高铁、网购、移动支付和共享单车被誉为中国的“新四大发明”,彰显出中国式创新的强劲活力.某移动支付公司从我市移动支付用户中随机抽取100名进行调查,得到如下数据:
每周移动支付次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 10 | 8 | 7 | 3 | 2 | 15 |
女 | 5 | 4 | 6 | 4 | 6 | 30 |
合计 | 15 | 12 | 13 | 7 | 8 | 45 |
(Ⅰ)把每周使用移动支付超过3次的用户称为“移动支付活跃用户”,能否在犯错误概率不超过0.005的前提下,认为是否为“移动支付活跃用户”与性别有关?
(Ⅱ)把每周使用移动支付6次及6次以上的用户称为“移动支付达人”,视频率为概率,在我市所有“移动支付达人”中,随机抽取4名用户.
①求抽取的4名用户中,既有男“移动支付达人”又有女“移动支付达人”的概率;
②为了鼓励男性用户使用移动支付,对抽出的男“移动支付达人”每人奖励300元,记奖励总金额为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附公式及表如下:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【答案】(Ⅰ)在犯错误概率不超过0.005的前提下,能认为是否为“移动支付活跃用户”与性别有关.(Ⅱ)①![]() ②见解析.
②见解析.
【解析】分析:(Ⅰ)由题意完成列联表,结合列联表计算可得![]() .所以在犯错误概率不超过0.005的前提下,能认为是否为“移动支付活跃用户”与性别有关.
.所以在犯错误概率不超过0.005的前提下,能认为是否为“移动支付活跃用户”与性别有关.
(Ⅱ)视频率为概率,在我市“移动支付达人”中,随机抽取1名用户,该用户为男“移动支付达人”的概率为![]() ,女“移动支付达人”的概率为
,女“移动支付达人”的概率为![]() .
.
①有对立事件公式可得满足题意的概率值为![]() .
.
②记抽出的男“移动支付达人”人数为![]() ,则
,则![]() .由题意得
.由题意得![]() ,由二项分布公式首先求得Y的分布列,然后利用均值和方差的性质可得X的分布列,计算可得
,由二项分布公式首先求得Y的分布列,然后利用均值和方差的性质可得X的分布列,计算可得![]() ,得
,得![]() 的数学期望
的数学期望![]() 元.
元.
详解:(Ⅰ)由表格数据可得![]() 列联表如下:
列联表如下:
非移动支付活跃用户 | 移动支付活跃用户 | 合计 | |
男 | 25 | 20 | 45 |
女 | 15 | 40 | 55 |
合计 | 40 | 60 | 100 |
将列联表中的数据代入公式计算得:
![]()
![]() .
.
所以在犯错误概率不超过0.005的前提下,能认为是否为“移动支付活跃用户”与性别有关.
(Ⅱ)视频率为概率,在我市“移动支付达人”中,随机抽取1名用户,
该用户为男“移动支付达人”的概率为![]() ,女“移动支付达人”的概率为
,女“移动支付达人”的概率为![]() .
.
①抽取的4名用户中,既有男“移动支付达人”,又有女“移动支付达人”的概率为![]() .
.
②记抽出的男“移动支付达人”人数为![]() ,则
,则![]() .
.
由题意得![]() ,
,
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
所以![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
所以![]() 的分布列为
的分布列为
| 0 | 300 | 600 | 900 | 1200 |
|
|
|
|
|
|
由![]() ,得
,得![]() 的数学期望
的数学期望![]() 元.
元.

【题目】某校为确定数学成绩与玩手机之间的关系,从全校随机抽样调查了40名同学,其中40%的人玩手机.这40位同学的数学分数(百分制)的茎叶图如图①所示.数学成绩不低于70分为良好,低于70分为一般.
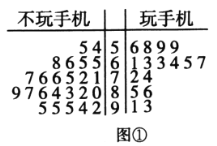
(1)根据以上资料完成下面的![]() 列联表,并判断有多大把握认为“数学成绩良好与不玩手机有关系”.
列联表,并判断有多大把握认为“数学成绩良好与不玩手机有关系”.
数学成绩良好 | 数学成绩一般 | 总计 | |
不玩手机 | |||
玩手机 | |||
总计 | 40 |
(2)现将40名同学的数学成绩分为如下5组:
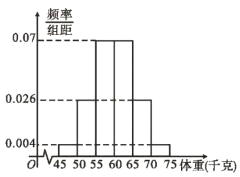
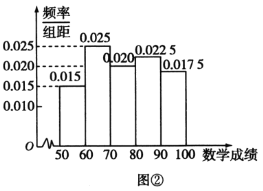
![]() ,其频率分布直方图如图②所示.计算这40名同学数学成绩的平均数,由茎叶图得到的真实值记为
,其频率分布直方图如图②所示.计算这40名同学数学成绩的平均数,由茎叶图得到的真实值记为![]() ,由频率分布直方图得到的估计值记为
,由频率分布直方图得到的估计值记为![]() (同一组中的数据用该组区间的中点值作代表),求
(同一组中的数据用该组区间的中点值作代表),求![]() 与
与![]() 的误差值.
的误差值.
(3)从这40名同学数学成绩高于90分的7人中随机选取2人,求至少有一人玩手机的概率.
附:![]() ,
,
这40名同学的数学成绩总和为2998分.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |