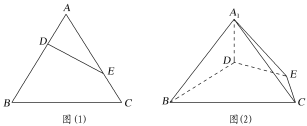
题目内容
【题目】等边![]() 的边长为
的边长为![]() ,点
,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,且满足
上的点,且满足![]() (如图(1)),将
(如图(1)),将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使二面角
的位置,使二面角![]() 成直二面角,连接
成直二面角,连接![]() ,
,![]() (如图(2)).
(如图(2)).
(1)求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】(1)证明见解析;(2)存在点![]() ,
,![]() .
.
【解析】
(1)通过证明![]() ,
,![]() 即可证明
即可证明![]() 平面
平面![]() ;(2)以
;(2)以![]() 为坐标原点,以射线
为坐标原点,以射线![]() 、
、![]() 、
、![]() 分别为
分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴的正半轴建立空间直角坐标系
轴的正半轴建立空间直角坐标系![]() ,设
,设![]() ,然后并求出平面
,然后并求出平面![]() 的一个法向量及
的一个法向量及![]() 的坐标,最后根据
的坐标,最后根据 即可求出
即可求出![]() 的值及
的值及![]() 的长度.
的长度.
(1)证明 题图(1)中,由已知可得:
![]() ,
,![]() ,
,![]() .
.
从而![]() .
.
故得![]() ,所以
,所以![]() ,
,![]() .
.
所以题图(2)中,![]() ,
,![]() ,
,
所以![]() 为二面角
为二面角![]() 的平面角,
的平面角,
又二面角![]() 为直二面角,
为直二面角,
所以![]() ,即
,即![]() ,
,
因为![]() 且
且![]() 、
、![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)解 存在.由(1)知![]() ,
,![]() 平面
平面![]() .
.
以![]() 为坐标原点,以射线
为坐标原点,以射线![]() 、
、![]() 、
、![]() 分别为
分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴的正半轴建立空间直角坐标系
轴的正半轴建立空间直角坐标系![]() ,如图,
,如图,
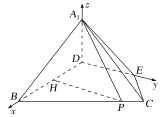
过![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
易知![]() ,
,![]() ,
,![]() ,
,
所以![]() .
.
因为![]() 平面
平面![]() ,
,
所以平面![]() 的一个法向量为
的一个法向量为![]() .
.
因为直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,所以
,所以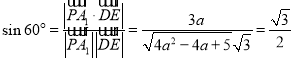 ,解得
,解得![]() .
.
所以![]() ,满足
,满足![]() ,符合题意.
,符合题意.
所以在线段![]() 上存在点
上存在点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,此时
,此时![]() .
.

练习册系列答案
相关题目
【题目】作为交通重要参与者的行人,闯红灯通行频有发生,带来了较大的交通安全隐患.在某十字路口,交警部门从穿越该路口的行人中随机抽取了200人进行调查,得到不完整的![]() 列联表如图所示:
列联表如图所示:
年龄低于30岁 | 年龄不低于30岁 | 合计 | |
闯红灯 | 60 | 80 | |
未闯红灯 | 80 | ||
合计 | 200 |
(1)将![]() 列联表补充完整;
列联表补充完整;
(2)是否有99.9%的把握认为行人是否闯红灯与年龄有关.
参考公式及数据: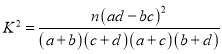 ,其中
,其中![]() .
.
P( | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |