题目内容
【题目】已知![]() 是椭圆
是椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆
在椭圆![]() 上,且离心率为
上,且离心率为![]()
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 的角平分线所在的直线
的角平分线所在的直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() 为椭圆
为椭圆![]() 上的一点,当
上的一点,当![]() 面积最大时,求点
面积最大时,求点![]() 的坐标.
的坐标.
【答案】(1) ![]() (2)
(2) 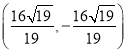
【解析】试题分析:(1)由椭圆![]() 经过点
经过点![]() ,离心率
,离心率![]() ,列方程求解
,列方程求解![]() 的值,即可得到椭圆的方程;
的值,即可得到椭圆的方程;
(2)由(1)可得直线![]() 和
和![]() 的方程,设
的方程,设![]() 为直线
为直线![]() 上任意一点,解得直线
上任意一点,解得直线![]() 的方程,
的方程,
设过![]() 点且平行于
点且平行于![]() 的直线
的直线![]() ,联立方程组
,联立方程组![]() ,求得实数
,求得实数![]() 的值,进而得到点
的值,进而得到点![]() 的坐标.
的坐标.
试题解析:
(1)由椭圆![]() 经过点
经过点![]() ,离心率
,离心率![]() ,可得
,可得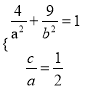 ,解得
,解得
![]() ,所以椭圆的标准方程为
,所以椭圆的标准方程为![]()
(2)由(1)可知![]() ,则直线
,则直线![]() 的方程
的方程![]() ,即
,即![]()
直线![]() 的方程
的方程![]() ,由点A在椭圆
,由点A在椭圆![]() 上的位置易知直线
上的位置易知直线![]() 的斜率为正数,
的斜率为正数,
设![]() 为直线
为直线![]() 上任意一点,则
上任意一点,则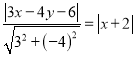 ,解得
,解得![]() 或
或
![]() (斜率为负数,舍去)
(斜率为负数,舍去)
![]() 直线
直线![]() 的方程为
的方程为![]() ,设过
,设过![]() 点且平行于
点且平行于![]() 的直线为
的直线为![]()
由 ,整理得
,整理得![]()
由![]() ,解得
,解得![]() ,因为
,因为![]() 为直线
为直线![]() 在
在![]() 轴上的截距,依题意,
轴上的截距,依题意, ![]() ,故
,故![]()
解得![]() ,
, ![]() ,所以
,所以![]() 点的坐标为
点的坐标为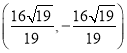

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】2017年5月14日,第一届“一带一路”国际高峰论坛在北京举行,为了解不同年龄的人对“一带一路”关注程度,某机构随机抽取了年龄在15-75岁之间的100人进行调查, 经统计“青少年”与“中老年”的人数之比为9:11
关注 | 不关注 | 合计 | |
青少年 | 15 | ||
中老年 | |||
合计 | 50 | 50 | 100 |
(1)根据已知条件完成上面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为关注“一带一路”是否和年龄段有关?
的把握认为关注“一带一路”是否和年龄段有关?
(2)现从抽取的青少年中采用分层抽样的办法选取9人进行问卷调查.在这9人中再选取3人进行面对面询问,记选取的3人中关注“一带一路”的人数为X,求X的分布列及数学期望.
附:参考公式 ,其中
,其中![]()
临界值表:
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |