Question

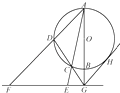
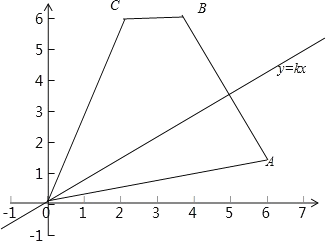
【题目】四边形OABC的四个顶点坐标分别为O(0,0)、A(6,2)、B(4,6)、C(2,6)，直线y＝kx(<k<3)分四边形OABC为两部分，S表示靠近x轴一侧的那一部分的面积．

(1)求S＝f(k)的函数表达式；

(2)当k为何值时，直线y＝kx将四边形OABC分为面积相等的两部分？

Answer 1

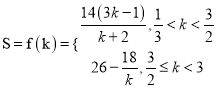【答案】（1）；（2）.

【解析】试题分析：（1）由题意画出图象，讨论当，此时要求的面积为三角形，由|OA|及交点到直线OA的距离求解即可；当此时要求的面积为四边形，以OB为底边分成上下两个三角形求面积和即可；
（2）由（1）和条件列出方程求出k的值．

试题解析：

(1)因为，所以需分两种情况：

①<k<时，直线y＝kx与直线AB：2x＋y＝14相交．

由得交点P1(，)，

又点P1到直线OA：x－3y＝0的距离为

d＝，

∴S＝|OA|·d＝.

②当≤k<3时，直线y＝kx与直线BC：y＝6交于P2(，6)．∴S△OP2C＝|P2C|·6＝.

又S△OAB＋S△OBC＝S四边形OABC＝20.

∴S＝20－＝26－.

故S＝f(k)＝

(2)若直线y＝kx平分四边形OABC的面积，

由(1)知，只需＝10，解得k＝.