题目内容
【题目】如图,AB是圆O的直径,G是AB延长线上的一点,GCD是圆O的割线,过点G作AG的垂线,交直线AC于点E,交直线 AD于点F,过点G作圆O的切线,切点为H. 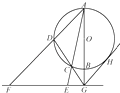
(1)求证:C,D,E,F四点共圆;
(2)若GH=8,GE=4,求EF的长.
【答案】
(1)解:连接DB,
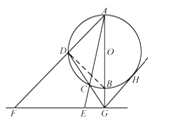
∵AB是⊙O的直径,∴∠ADB=90°,
在Rt△ABD和Rt△AFG中,∠ABD=∠AFE,
又∵∠ABD=∠ACD,∠ACD=∠AFE.
∴C,D,E,F四点共圆;
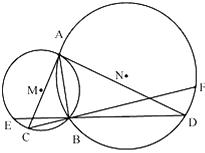
(2)解:∵C,D,E,F四点共圆,∴GEGF=GCGD.
∵GH是⊙O的切线,∴GH2=GCGD,∴GH2=GEGF.
又因为GH=8,GE=4,所以GF=16.
∴EF=GF﹣GE=12.
【解析】(1)连接DB,利用AB是⊙O的直径,可得∠ADB=90°,在Rt△ABD和Rt△AFG中,∠ABD=∠AFE,又同弧所对的圆周角相等可得∠ACD=∠ABD,进而得到∠ACD=∠AFE即可证明四点共圆;(2)由C,D,E,F四点共圆,利用共线定理可得GEGF=GCGD.由GH是⊙O的切线,利用切割线定理可得GH2=GCGD,进而得到GH2=GEGF即可.

【题目】据IEC(国际电工委员会)调查显示,小型风力发电项目投资较少,且开发前景广阔,但受风力自然资源影响,项目投资存在一定风险.根据测算,风能风区分类标准如下:
风能分类 | 一类风区 | 二类风区 |
平均风速m/s | 8.5~10 | 6.5~8.5 |
假设投资A项目的资金为x(x≥0)万元,投资B项目资金为y(y≥0)万元,调研结果是:未来一年内,位于一类风区的A项目获利30%的可能性为0.6,亏损20%的可能性为0.4;位于二类风区的B项目获利35%的可能性为0.6,亏损10%的可能性是0.1,不赔不赚的可能性是0.3.
(1)记投资A,B项目的利润分别为ξ和η,试写出随机变量ξ与η的分布列和期望Eξ,Eη;
(2)某公司计划用不超过100万元的资金投资于A,B项目,且公司要求对A项目的投资不得低于B项目,根据(1)的条件和市场调研,试估计一年后两个项目的平均利润之和z=Eξ+Eη的最大值.
【题目】某土特产销售总公司为了解其经营状况,调查了其下属各分公司月销售额和利润,得到数据如下表:
分公司名称 | 雅雨 | 雅雨 | 雅女 | 雅竹 | 雅茶 |
月销售额x(万元) | 3 | 5 | 6 | 7 | 9 |
月利润y(万元) | 2 | 3 | 3 | 4 | 5 |
在统计中发现月销售额x和月利润额y具有线性相关关系.
(Ⅰ)根据如下的参考公式与参考数据,求月利润y与月销售额x之间的线性回归方程;
(Ⅱ)若该总公司还有一个分公司“雅果”月销售额为10万元,试求估计它的月利润额是多少?(参考公式: ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() ,其中:
,其中: ![]() =112,
=112, ![]() =200).
=200).
