Question

【题目】设是定义在上的奇函数，当时， .

（1）求的解析式；

（2）解不等式.

Answer 1

【答案】(1) 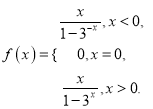；(2)(－∞，－2)∪(0,2)．

【解析】试题分析：（1）奇函数有f(0)＝0，再由x<0时，f(x)＝－f(－x)即可求解；

（2）由（1）分段求解不等式，最后取并集即可.

试题解析：

（1）因为f(x)是定义在上的奇函数，所以当x=0时，f(x)＝0，

当x<0时，f(x)＝－f(－x)，－x>0，又因为当x>0时，f(x)＝，.

所以当x<0时，f(x)＝－f(－x)＝－＝..

综上所述：此函数的解析式.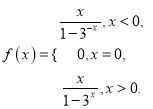

（2）f(x)<－，当x=0时，f(x)<－不成立；

当x>0时，即<－，所以<－，所以>，所以3x－1<8，解得x<2，

当x<0时，即<－，所以>－，所以3－x>32，所以x<－2，

综上所述解集是(－∞，－2)∪(0,2)．