题目内容
13.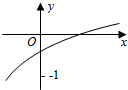 函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )
函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )| A. | 0<a-1<b-1<1 | B. | 0<b-1<a<1 | C. | 0<b<a-1<1 | D. | 0<a-1<b<1 |
分析 利用对数函数和函数图象平移的方法列出关于a,b的不等关系是解决本题的关键.利用好图形中的标注的(0,-1)点.利用复合函数思想进行单调性的判断,进而判断出底数与1的大小关系.
解答 解:∵函数f(x)=loga(2x+b-1)是增函数,
令t=2x+b-1,必有t=2x+b-1>0,
t=2x+b-1为增函数.
∴a>1,∴0<$\frac{1}{a}$<1,
∵当x=0时,f(0)=logab<0,
∴0<b<1.
又∵f(0)=logab>-1=loga$\frac{1}{a}$,
∴b>$\frac{1}{a}$,
∴0<a-1<b<1.
故选:D.
点评 本题考查对数函数的图象性质,考查学生的识图能力.考查学生的数形结合能力和等价转化思想.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
4.如果满足9x-a≥0>8x-b的实数x的整数值只有1,2,3,那么满足这个条件的整式a,b的有序实数对(a,b)共有( )
| A. | 48对 | B. | 63对 | C. | 64对 | D. | 72对 |
1.命题p:$\overrightarrow{AB}$•$\overrightarrow{AC}$<0,命题q:∠BAC是钝角.p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.已知某个车轮旋转的角度α(弧度)与时间t(秒)的函数关系是α=$\frac{2π}{0.64}$t2(t≥0),则车轮启动后第1.6秒时的瞬时角速度是( )
| A. | 20π弧度/秒 | B. | 10π弧度/秒 | C. | 8π弧度/秒 | D. | 5π弧度/秒 |
2.若点(-2,-1)是圆(x+1)2+y2=1的弦AB的中点,则直线AB的方程为( )
| A. | x-y+1=0 | B. | 3x+y+7=0 | C. | x+y+3=0 | D. | x-3y-1=0 |
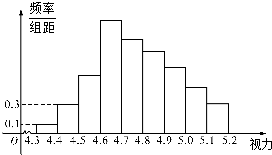 某医院眼科某天测量300名求医者的视力情况,得到频率分布直方图如图所示,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列.
某医院眼科某天测量300名求医者的视力情况,得到频率分布直方图如图所示,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列.