题目内容

3．已知an=log（n+1）（n+2），（n∈N*），我们把使乘积a1，a2，a3，…an为整数的数n叫做“劣数”，则在区间（15，2015）内的所有劣数的和为2004．

分析 利用对数的换底公式可得：a1•a2•a3•…•an=$\frac{lg3}{lg2}×\frac{lg4}{lg3}$×…×$\frac{lg（n+2）}{lg（n+1）}$=log2（n+2），要使log2（n+2）为整数，则n+2必须为2k（k∈N*）形式的数，即可得出．

解答 解：a1•a2•a3•…•an=$\frac{lg3}{lg2}×\frac{lg4}{lg3}$×…×$\frac{lg（n+2）}{lg（n+1）}$=log2（n+2），
要使log2（n+2）为整数，则n+2必须为2k（k∈N*）形式的数，
∴在区间（15，2015）内的所有劣数为30，62，126，254，510，1022，
其和=30+62+126+254+510+1022=2004，
故答案为：2004．

点评 本题考查了对数的换底公式、2k（k∈N*）形式的数，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
13．已知函数f（x）=lg（x+1），g（x）=2lg（2x+t）（t为参数）．
（1）写出函数f（x）的定义域和值域；
（2）当x∈[0，1]时，如果f（x）≤g（x），求参数t的取值范围．
14．已知向量$\vec a$、$\vec b$满足|${\vec a$+$\vec b}$|=5，$\vec a$•$\vec b$=4，则|${\vec a$-$\vec b}$|=3．
11．已知动圆过定点F（1，0）且与直线?1：x=-1相切．
（Ⅰ）求动圆圆心的轨迹C的方程；
（Ⅱ）设直线?：y=-$\frac{1}{2}$x+b与轨迹C交于A，B两点，若x轴与以AB为直径的圆相切，求该圆的方程．
18．设b，c表示两条直线，α，β表示两个平面，则下列命题正确的是（　　）
A．若b?α，c∥α，则c∥bB．若c∥α，c⊥β，则α⊥βC．若c∥α，α⊥β，则c⊥βD．若b?α，b∥c，则c∥α
8．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}x，0＜x≤2}\\{-|x-3|，x＞2}\end{array}\right.$，若方程f（x）=ax+1有三个不同的实数根，则实数a的取值范围是（　　）
A．（-1，-$\frac{1}{3}$）B．（-1，-$\frac{1}{3}$]C．（-∞，-1）∪[-$\frac{1}{3}$，+∞）D．（-∞，-1）∪（-$\frac{1}{3}$，+∞）
15．已知函数f（x）=ex-$\frac{1}{2}{x^2}$-ax+b在x=0处的切线方程为y=-2x+4．
（1）求函数f（x）的解析式．
（2）证明：?x1，x2∈R且x1≠x2，恒有$\frac{{f（{x_1}）-f（{x_2}）}}{{{x_1}-{x_2}}}$＞-2成立．
12．已知下列三个正确的结论：
①在△ABC中，不等式$\frac{1}{A}$+$\frac{1}{B}$+$\frac{1}{C}$≥$\frac{9}{π}$成立
②在四边形ABCD中，不等式$\frac{1}{A}$+$\frac{1}{B}$+$\frac{1}{C}$+$\frac{1}{D}$≥$\frac{16}{2π}$成立
③在五边形ABCDE中，不等式$\frac{1}{A}$+$\frac{1}{B}$+$\frac{1}{C}$+$\frac{1}{D}$+$\frac{1}{E}$≥$\frac{25}{3π}$成立．
（1）猜想在n边形A1，A2，…An中，有怎样的不等式成立？
（2）证明：在△ABC中，不等式$\frac{1}{A}$+$\frac{1}{B}$+$\frac{1}{C}$≥$\frac{9}{π}$成立．
13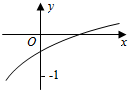．函数f（x）=loga（2x+b-1）（a＞0，a≠1）的图象如图所示，则a，b满足的关系是（　　）
A．0＜a-1＜b-1＜1B．0＜b-1＜a＜1C．0＜b＜a-1＜1D．0＜a-1＜b＜1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网