题目内容
18.已知函数f(x)=$\frac{2{a}^{x}}{{a}^{x}-1}$+loga$\frac{x-1}{x+1}$(a>0且a≠1),且f(m)=7(m≠0),则f(-m)=-5.分析 构造函数g(x)=f(x)-2,得到f(x)=-g(-x),代入即可得到f(-m)的值.
解答 解:设g(x)=f(x)-2=$\frac{2{a}^{x}}{{a}^{x}-1}$+loga$\frac{x-1}{x+1}$-2=$\frac{2}{{a}^{x}-1}$+loga$\frac{x-1}{x+1}$,
∴g(-x)=$\frac{2}{{a}^{-x}-1}$+loga$\frac{x+1}{x-1}$=-$\frac{2{a}^{x}}{{a}^{x}-1}$-loga$\frac{x-1}{x+1}$=-f(x),
∴f(x)=-g(-x),g(x)=f(x)-2,
∴f(-m)=-g(m)=-f(m)+2=-7+2=-5,
故答案为:-5
点评 本题考查了函数的奇偶性的应用,关键是构造函数g(x)=f(x)-2,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}x,0<x≤2}\\{-|x-3|,x>2}\end{array}\right.$,若方程f(x)=ax+1有三个不同的实数根,则实数a的取值范围是( )
| A. | (-1,-$\frac{1}{3}$) | B. | (-1,-$\frac{1}{3}$] | C. | (-∞,-1)∪[-$\frac{1}{3}$,+∞) | D. | (-∞,-1)∪(-$\frac{1}{3}$,+∞) |
6.定义在(0,+∞)的函数f(x)为单调函数,对任意的x∈(0,+∞)恒有f[f(x)-log4x]=5.x0是方程f(x)-f′(x)=4的一个根,则x0所在区间为( )
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
13.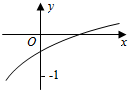 函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )
函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )
 函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )
函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )| A. | 0<a-1<b-1<1 | B. | 0<b-1<a<1 | C. | 0<b<a-1<1 | D. | 0<a-1<b<1 |
3.在空间中,设直线l的方向向量为$\overrightarrow{a}$,平面α的法向量为$\overrightarrow{b}$,对于原命题“若$\overrightarrow{a}$•$\overrightarrow{b}$=0,则l∥α”,下列判断正确的是( )
| A. | 原命题为真,否命题为真 | B. | 原命题为假,否命题为假 | ||
| C. | 原命题为假,否命题为真 | D. | 原命题为真,否命题为假 |
7.抛物线y2=4x的焦点为F,原点为O,直线AB经过点F且与抛物线交于A,B两点,抛物线的准线与x轴交于点C,若∠OFA=135°,则tan∠ACB=( )
| A. | 2$\sqrt{2}$ | B. | $\frac{4\sqrt{2}}{5}$ | C. | $\frac{4\sqrt{2}}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |