题目内容
1.命题p:$\overrightarrow{AB}$•$\overrightarrow{AC}$<0,命题q:∠BAC是钝角.p是q的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据充分条件和必要条件的定义结合向量数量积的应用进行判断即可.
解答 解:若$\overrightarrow{AB}$•$\overrightarrow{AC}$<0,即|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|cos∠BAC<0,
即-1≤cos∠BAC<0,则$\frac{π}{2}$<∠BAC≤π,则∠BAC是钝角不一定成立,
反之若∠BAC是钝角,则cos∠BAC<0,即$\overrightarrow{AB}$•$\overrightarrow{AC}$=|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|cos∠BAC<0,
则$\overrightarrow{AB}$•$\overrightarrow{AC}$<0成立,
即p是q的必要不充分条件,
故选:B.
点评 本题主要考查充分条件和必要条件的判断,利用向量数量积的定义是解决本题的关键.

练习册系列答案
相关题目
6.定义在(0,+∞)的函数f(x)为单调函数,对任意的x∈(0,+∞)恒有f[f(x)-log4x]=5.x0是方程f(x)-f′(x)=4的一个根,则x0所在区间为( )
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
13.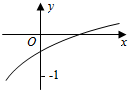 函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )
函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )
 函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )
函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )| A. | 0<a-1<b-1<1 | B. | 0<b-1<a<1 | C. | 0<b<a-1<1 | D. | 0<a-1<b<1 |