题目内容
8. 某医院眼科某天测量300名求医者的视力情况,得到频率分布直方图如图所示,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列.
某医院眼科某天测量300名求医者的视力情况,得到频率分布直方图如图所示,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列.(1)求出最大频率;
(2)求出视力在4.6-5.0的人数.
分析 (1)根据频率分布直方图,得出4.6~4.7间的频率最大,利用频数、等比数列的知识求出最大频率值;
(2)根据后6组的频数成等差数列,且和为261,求出公差d,即可计算所求的结果.
解答 解:(1)根据频率分布直方图,得组距为0.1,
则4.3~4.4间的频数为300×0.1×0.1=3;
4.4~4.5间的频数为300×0.1×0.3=9,
所以4.6~4.7间的频率最大,为3×33=81,
所以最大频率为0.27;
(2)根据后6组的频数成等差数列,且共有300-39=261人,
设公差为d,则6×81+$\frac{6×5}{2}$•d=261,
解得d=-15;
所以视力在4.6~5.0的人数为:
4×81+$\frac{4×3}{2}$×(-15)=234.
点评 本题考查了频率分布直方图的应用问题,也考查了等差与等比数列的应用问题,是综合性题目.

练习册系列答案
相关题目
18.设b,c表示两条直线,α,β表示两个平面,则下列命题正确的是( )
| A. | 若b?α,c∥α,则c∥b | B. | 若c∥α,c⊥β,则α⊥β | C. | 若c∥α,α⊥β,则c⊥β | D. | 若b?α,b∥c,则c∥α |
3.a,b,c,d四位同学各自对甲、乙两变量做回归分析,分别得到散点图与残差平方和$\sum_{i=1}^{n}$(yi-$\widehat{{y}_{i}}$)2如下表:
哪位同学的实验结果体现拟合甲、乙两变量关系的模型拟合精度高?( )
| a | b | c | d | |
| 散点图 |  | 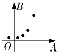 |  |  |
| 残差平方和 | 115 | 106 | 124 | 103 |
| A. | a | B. | b | C. | c | D. | d |
13.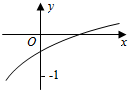 函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )
函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )
 函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )
函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )| A. | 0<a-1<b-1<1 | B. | 0<b-1<a<1 | C. | 0<b<a-1<1 | D. | 0<a-1<b<1 |
17.设集合A=[-1,2],B={x|1≤x≤4},则A∩B=( )
| A. | {x|0≤x≤2} | B. | {x|1≤x≤2} | C. | {x|0≤x≤4} | D. | {x|1≤x≤4} |