题目内容

4．如果满足9x-a≥0＞8x-b的实数x的整数值只有1，2，3，那么满足这个条件的整式a，b的有序实数对（a，b）共有（　　）
A．48对B．63对C．64对D．72对

分析 先解不等式组得到x的范围，再根据x的整数值得到a，b的范围，根据分步计数原理得到有序实数对．

解答 解：解不等式组9x-a≥0＞8x-b得$\frac{a}{9}$≤x＜$\frac{b}{8}$，
∵实数x的整数值只有1，2，3，
∴0＜$\frac{a}{9}$≤1，3＜$\frac{b}{8}$≤4，
解得0＜a≤9，24＜b≤32，
∴a的整数解有9个，b的整数解有8个，
∴a，b的有序实数对（a，b）共有9×8=72对，
故选：D

点评 本题考查不等式得解法和应用，属于基础题．

练习册系列答案
相关题目
14．已知向量$\vec a$、$\vec b$满足|${\vec a$+$\vec b}$|=5，$\vec a$•$\vec b$=4，则|${\vec a$-$\vec b}$|=3．
15．已知函数f（x）=ex-$\frac{1}{2}{x^2}$-ax+b在x=0处的切线方程为y=-2x+4．
（1）求函数f（x）的解析式．
（2）证明：?x1，x2∈R且x1≠x2，恒有$\frac{{f（{x_1}）-f（{x_2}）}}{{{x_1}-{x_2}}}$＞-2成立．
12．已知下列三个正确的结论：
①在△ABC中，不等式$\frac{1}{A}$+$\frac{1}{B}$+$\frac{1}{C}$≥$\frac{9}{π}$成立
②在四边形ABCD中，不等式$\frac{1}{A}$+$\frac{1}{B}$+$\frac{1}{C}$+$\frac{1}{D}$≥$\frac{16}{2π}$成立
③在五边形ABCDE中，不等式$\frac{1}{A}$+$\frac{1}{B}$+$\frac{1}{C}$+$\frac{1}{D}$+$\frac{1}{E}$≥$\frac{25}{3π}$成立．
（1）猜想在n边形A1，A2，…An中，有怎样的不等式成立？
（2）证明：在△ABC中，不等式$\frac{1}{A}$+$\frac{1}{B}$+$\frac{1}{C}$≥$\frac{9}{π}$成立．
19．在直角坐标平面上有一点列P1（x1，y1），P2（x2，y2），…，Pn（xn，yn），…，对每个正整数n，点Pn位于函数y=3x+$\frac{13}{4}$的图象上，且Pn的横坐标构成以-$\frac{5}{2}$为首项，-1为公差的等差数列{xn}．
（1）求点Pn的坐标；
（2）设抛物线列C1，C2，C3，…，Cn，…中的每一条的对称轴都垂直于x轴，第n条抛物线Cn的顶点为Pn且过点Dn（0，n2+1），记过点Dn且与抛物线Cn相切的直线
的斜率为kn，求证：$\frac{1}{k{{{\;}_{1}k}_{2}}_{\;}}$+$\frac{1}{{k}_{2}{k}_{3}}$+…+$\frac{1}{{{k}_{n-1}}_{\;}{k}_{n}}$＜$\frac{1}{10}$．
9．f（x）=-$\frac{1}{2}$x2+bln（x+2）在（-1，+∞）上单调递减，则b的取值范围为（-∞，-1]．
16．某水厂的蓄水池中有400吨水，每天零点开始由池中放水向居民供水，同时以每小时60吨的速度向池中注水，若t小时内向居民供水总量为100$\sqrt{6t}$（0≤t≤24），则每天$\frac{25}{6}$点时蓄水池中的存水量最少．
13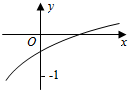．函数f（x）=loga（2x+b-1）（a＞0，a≠1）的图象如图所示，则a，b满足的关系是（　　）
A．0＜a-1＜b-1＜1B．0＜b-1＜a＜1C．0＜b＜a-1＜1D．0＜a-1＜b＜1
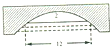14．一座圆形拱桥，当水面在如图所示位置时，拱桥离水面2米，水面宽12米，当水面下降1米后水面宽为2$\sqrt{51}$米．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网