题目内容
2.若点(-2,-1)是圆(x+1)2+y2=1的弦AB的中点,则直线AB的方程为( )| A. | x-y+1=0 | B. | 3x+y+7=0 | C. | x+y+3=0 | D. | x-3y-1=0 |
分析 求出圆心C的坐标,得到PC的斜率,利用中垂线的性质求得直线AB的斜率,点斜式写出AB的方程,并化为一般式.
解答 解:圆(x+1)2+y2=1的圆心C(-1,0),
点P(-2,-1)为 弦AB的中点,
PC的斜率为 $\frac{0-(-1)}{-1-(-2)}$=1,
由AB⊥PC,可得直线AB的斜率为-1,
点斜式写出直线AB的方程y+1=-1•(x+2),
即x+y+3=0,
故选C.
点评 本题考查直线和圆相交的性质,线段的中垂线的性质,用点斜式求直线的方程的方法.

练习册系列答案
相关题目
13.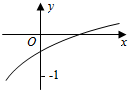 函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )
函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )
 函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )
函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )| A. | 0<a-1<b-1<1 | B. | 0<b-1<a<1 | C. | 0<b<a-1<1 | D. | 0<a-1<b<1 |
17.设集合A=[-1,2],B={x|1≤x≤4},则A∩B=( )
| A. | {x|0≤x≤2} | B. | {x|1≤x≤2} | C. | {x|0≤x≤4} | D. | {x|1≤x≤4} |
7.抛物线y2=4x的焦点为F,原点为O,直线AB经过点F且与抛物线交于A,B两点,抛物线的准线与x轴交于点C,若∠OFA=135°,则tan∠ACB=( )
| A. | 2$\sqrt{2}$ | B. | $\frac{4\sqrt{2}}{5}$ | C. | $\frac{4\sqrt{2}}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
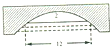 一座圆形拱桥,当水面在如图所示位置时,拱桥离水面2米,水面宽12米,当水面下降1米后水面宽为2$\sqrt{51}$米.
一座圆形拱桥,当水面在如图所示位置时,拱桥离水面2米,水面宽12米,当水面下降1米后水面宽为2$\sqrt{51}$米.