题目内容
设0<x<1,a,b都为大于零的常数,若
+
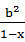≥m恒成立,则m的最大值
是 ( )
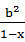+≥m恒成立,则m的最大值是 ( )
| A．( a-b)2 | B．(a+b)2 |
| C．a2b2 | D．a2 |
B
【解题指南】本题的关键是利用x+(1-x)=1结合基本不等式加以求解.
解:选B.由
+=
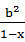[x+(1-x)]=a2+b2+
+
≥a2+b2+2ab=(a+b)2,
当且仅当
=时等号成立,所以m≤(a+b)2,m的最大值为(a+b)2.
练习册系列答案
相关题目
，
，
，
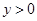．求证
．
=
”的证明过程:“等式两边同时乘以
得,左边=
=
=1,右边=1,左边=右边,故原不等式成立”,应用了
<1”的 ( )