题目内容
若{an}是各项为正的等比数列,且公比q≠1,则a1+a4与a2+a3的大小关系是 ( )
| A．a1+a4>a2+a3 | B．a1+a4<a2+a3 |
| C．a1+a4=a2+a3 | D．不确定 |
A
选A.(a1+a4)-(a2+a3)
=a1+a1q3-a1q-a1q2=a1(1+q)(1-q)2,
因为an>0,所以q>0,又q≠1,
所以a1(1+q)(1-q)2>0,即a1+a4>a2+a3.
=a1+a1q3-a1q-a1q2=a1(1+q)(1-q)2,
因为an>0,所以q>0,又q≠1,
所以a1(1+q)(1-q)2>0,即a1+a4>a2+a3.
练习册系列答案
名校课堂系列答案
相关题目
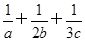＝m，求证：a＋2b＋3c≥9.
+
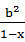≥m恒成立,则m的最大值
·
·
,则必有 ( )
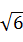
恒成立,则实数a的取范围是( )
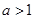
的解集为.