题目内容
【题目】已知椭圆![]() :
:![]() 的四个顶点围成的四边形的面积为
的四个顶点围成的四边形的面积为![]() ,其离心率为
,其离心率为![]()
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的右焦点
的右焦点![]() 作直线
作直线![]() (
(![]() 轴除外)与椭圆
轴除外)与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,在
,在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使
,使![]() 为定值?若存在,求出定点坐标及定值,若不存在,说明理由.
为定值?若存在,求出定点坐标及定值,若不存在,说明理由.
【答案】(1) ![]() (2)见解析
(2)见解析
【解析】
(1)由离心率及2ab=4![]() ,结合a2=b2+c2,解得a、b,即可求得椭圆C的方程;
,结合a2=b2+c2,解得a、b,即可求得椭圆C的方程;
(2)由题意可设直线l:x=my![]() ,代入椭圆方程,利用韦达定理及向量数量积的坐标运算,将
,代入椭圆方程,利用韦达定理及向量数量积的坐标运算,将![]()
![]() 用m与x0表示,利用对应系数成比例,即可求得x0,代入得
用m与x0表示,利用对应系数成比例,即可求得x0,代入得![]()
![]() 为定值;
为定值;
(1)由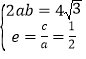 得:
得:![]() 所以椭圆方程为
所以椭圆方程为![]()
(2)由于直线l过右焦点F(1,0),可设直线l方程为:x=my+1,代入椭圆方程![]() 并整理得:(4+3m2)x2-8x+4-12m2=0(或(4+3m2)y2+6my-9=0)
并整理得:(4+3m2)x2-8x+4-12m2=0(或(4+3m2)y2+6my-9=0)
△=64-(4+3m2) (4-12m2)>0
设A(x1,y1),B(x2,y2),则x1,x2是方程①的两个解,
由韦达定理得:x1+x2=![]() , x1x2=
, x1x2=![]() ,y1+y2=
,y1+y2=![]() ,y1y2
,y1y2![]()
假设在x轴上存在定点P(x0,0),使![]() 为定值,则:
为定值,则:
(x1-x0)(x2-x0)+y1y2=x1x2+y1y2-x0(x1+x2)+x02=![]() +
+![]() -
-![]() +x02
+x02
=![]()
由题意,上式为定值,所以应有:![]()
即:12x02-48=-15-24x0+12x02
解得:x0=![]() ,
,
此时![]()

 全能测控期末小状元系列答案
全能测控期末小状元系列答案【题目】在全社会推行素质教育的大前提下,更强调了学生的全面发展,只有全面重视体育锻炼,才能使学生德智体美全面发展。为了解某高校大学生的体育锻炼情况,做了如下调查统计。该校共有学生10000人,其中男生6000人,女生4000人。为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集200位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
(2)根据这200个样本数据,得到学生每周平均体育运动时间的频率分布直方图,其中样本数据的分组区间为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,估计该校学生每周平均体育运动时间超过4个小时的概率.
,估计该校学生每周平均体育运动时间超过4个小时的概率.
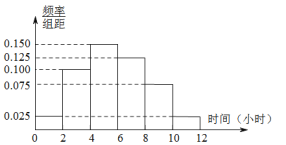
(3)在样本数据中,有50位女生的每周平均体育运动时间超过4个小时,请完成每周平均体育运动时间与性别的列联表,并判断能否在犯错误的概率不超过0.01的前提下认为“该校学生的每周平均体育运动时间与性别有关”.
女生 | 男生 | 总计 | |
每周平均体育运动时间不超过4小时 | |||
每周平均体育运动时间超过4小时 | |||
总计 |
附:![]()
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
【题目】为了解使用手机是否对学生的学习有影响,某校随机抽取100名学生,对学习成绩和使用手机情况进行了调查,统计数据如表所示(不完整):
使用手机 | 不使用手机 | 总计 | |
学习成绩优秀 | 10 | 40 | |
学习成绩一般 | 30 | ||
总计 | 100 |
(1)补充完整所给表格,并根据表格数据计算是否有99.9%的把握认为学生的学习成绩与使用手机有关;
(2)现从上表中不使用手机的学生中按学习成绩是否优秀分层抽样选出6人,再从这6人中随机抽取3人,求其中学习成绩优秀的学生恰有2人的概率.
参考公式: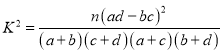 ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |