题目内容
【题目】在![]() 的方格表中取出46个方格染成红色.证明:存在一块由4个方格构成的
的方格表中取出46个方格染成红色.证明:存在一块由4个方格构成的![]() 区域,其中由至少3个方格被染成红色.
区域,其中由至少3个方格被染成红色.
【答案】见解析
【解析】
首先,考察![]() 的方格表.
的方格表.
如图,设第一行有![]() 个方格被染成红色,第2行有
个方格被染成红色,第2行有![]() 个方格被染成红色.
个方格被染成红色.
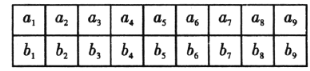
下面证明:若![]() ,则必存在一块由4个方格构成的
,则必存在一块由4个方格构成的![]() 区域,其中有至少3个方格被染成红色,若
区域,其中有至少3个方格被染成红色,若![]() ,则只有唯一的情形(如图)能够使得不存在由4个方格构成的
,则只有唯一的情形(如图)能够使得不存在由4个方格构成的![]() 区域,其中至少3个方格被染成红色.
区域,其中至少3个方格被染成红色.
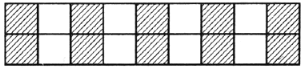
将![]() 方格表从左向右分成4个
方格表从左向右分成4个![]() 方格和一个
方格和一个![]() 区域.若不存在至少3个方格被染成红色的
区域.若不存在至少3个方格被染成红色的![]() 区域.则前4个
区域.则前4个![]() 方格中每个中至多有两个方格被染成红色,于是,总的红色方格数不超过
方格中每个中至多有两个方格被染成红色,于是,总的红色方格数不超过![]() ,矛盾.
,矛盾.
故当![]() 时,结论成立.
时,结论成立.
当![]() 时,必存在某一列的
时,必存在某一列的![]() 和
和![]() 同时被染成红色.为保证不存在
同时被染成红色.为保证不存在![]() 区域中至少3个方格不被染成红色,则要求
区域中至少3个方格不被染成红色,则要求![]() 和
和![]() 、
、![]() 和
和![]() 不被染成红色,显然,只有图中的情形满足.
不被染成红色,显然,只有图中的情形满足.
再回到本题.
假设存在某种染色方案使得![]() 方格表中不存在有至少3个方格被染成红色的
方格表中不存在有至少3个方格被染成红色的![]() 区域.
区域.
若该方案中存在相邻的两行(第![]() 行和第
行和第![]() 行)满足
行)满足![]() ,则必有
,则必有![]() .若
.若![]() 为奇数,则沿第
为奇数,则沿第![]() 行将方格表分成上、下两部分,上面有偶数行,下面也有偶数行,由前面的结论知,剩下的8行中至多有
行将方格表分成上、下两部分,上面有偶数行,下面也有偶数行,由前面的结论知,剩下的8行中至多有![]() 个方格被染成红色.于是,总的红色方格数不超过
个方格被染成红色.于是,总的红色方格数不超过![]() .若
.若![]() 为偶数,则沿第
为偶数,则沿第![]() 行划分,有相同的结论.
行划分,有相同的结论.
若任意相邻两行的红色方格数之和均不等于10,则
![]()
![]() .
.
因此,无论如何染色,要使![]() 方格表中不存在有至少3个方格被染成红色的
方格表中不存在有至少3个方格被染成红色的![]() 区域,最多只能有45个方格被染成红色,与题设矛盾.
区域,最多只能有45个方格被染成红色,与题设矛盾.
综上所述,必存在一块由4个方格构成的![]() 区域,其中有至少3个方格被染成红色.
区域,其中有至少3个方格被染成红色.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目