题目内容
【题目】在全社会推行素质教育的大前提下,更强调了学生的全面发展,只有全面重视体育锻炼,才能使学生德智体美全面发展。为了解某高校大学生的体育锻炼情况,做了如下调查统计。该校共有学生10000人,其中男生6000人,女生4000人。为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集200位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
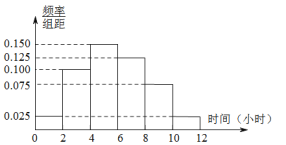
(2)根据这200个样本数据,得到学生每周平均体育运动时间的频率分布直方图,其中样本数据的分组区间为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,估计该校学生每周平均体育运动时间超过4个小时的概率.
,估计该校学生每周平均体育运动时间超过4个小时的概率.
(3)在样本数据中,有50位女生的每周平均体育运动时间超过4个小时,请完成每周平均体育运动时间与性别的列联表,并判断能否在犯错误的概率不超过0.01的前提下认为“该校学生的每周平均体育运动时间与性别有关”.
女生 | 男生 | 总计 | |
每周平均体育运动时间不超过4小时 | |||
每周平均体育运动时间超过4小时 | |||
总计 |
附:![]()
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
【答案】(1)应该收集80位女生的样本数据; (2)估计该校学生每周平均体育运动时间超过4小时的概率为0.75;(3)能在犯错误的概率不超过0.01的前提下认为“该校学生的每周体育运动的平均时间与性别有关”.
【解析】
(1)由题意,根据女生所占的比例,列出![]() ,即可求解;
,即可求解;
(2)根据频率方程直方图中概率的计算,即可求解200位学生每周平均体育运动时间超过4小时的频率;
(3)列出![]() 的列联表,利用公式求得
的列联表,利用公式求得![]() 的值,根据附表,即可判定.
的值,根据附表,即可判定.
(1)由题题,得![]() ,所以应该收集80位女生的样本数据,
,所以应该收集80位女生的样本数据,
(2)根据频率分布直方图,得200位学生每周平均体育运动时间超过4小时的频率为:
![]() .
.
因此可估计该校学生每周平均体育运动时间超过4小时的概率为0.75.
(3)列出![]() 的列联表,如下:
的列联表,如下:
女生 | 男生 | 合计 | |
每周平均体育运动时间不超过4小时 | 30 | 20 | 50 |
每周平均体育运动时间超过4小时 | 50 | 100 | 150 |
合计 | 80 | 120 | 200 |
![]() .
.
所以能在犯错误的概率不超过0.01的前提下认为“该校学生的每周体育运动的平均时间与性别有关”.

【题目】水稻是人类重要的粮食作物之一,耕种与食用的历史都相当悠久,日前我国南方农户在播种水稻时一般有直播、撒酒两种方式.为比较在两种不同的播种方式下水稻产量的区别,某市红旗农场于2019年选取了200块农田,分成两组,每组100块,进行试验.其中第一组采用直播的方式进行播种,第二组采用撒播的方式进行播种.得到数据如下表:
产量(单位:斤) 播种方式 | [840,860) | [860,880) | [880,900) | [900,920) | [920,940) |
直播 | 4 | 8 | 18 | 39 | 31 |
散播 | 9 | 19 | 22 | 32 | 18 |
约定亩产超过900斤(含900斤)为“产量高”,否则为“产量低”
(1)请根据以上统计数据估计100块直播农田的平均产量(同一组中的数据用该组区间的中点值为代表)
(2)请根据以上统计数据填写下面的2×2列联表,并判断是否有99%的把握认为“产量高”与“播种方式”有关?
产量高 | 产量低 | 合计 | |
直播 | |||
散播 | |||
合计 |
附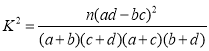 :
:
P(K2≥k0) | 0.10 | 0.010 | 0.001 |
k0 | 2.706 | 6.635 | 10.828 |