题目内容
圆心在抛物线x2=2y上,与直线2x+2y+3=0相切的圆中,求面积最小的圆的方程.
∵圆心在抛物线x2=2y上,∴可设圆心为(a,
a2),
又∵直线2x+2y+3=0与圆相切,
∴圆心到直线2x+2y+3=0的距离等于半径r,
即r=
=
=
≥
=
,
可得当a=-1时,半径r最小,
∴所有的圆中,面积最小圆的半径r=
,此时圆的圆心坐标为(-1,
).
因此,所求圆的方程为(x+1)2+(y-
)2=
.
| 1 |
| 2 |
又∵直线2x+2y+3=0与圆相切,
∴圆心到直线2x+2y+3=0的距离等于半径r,
即r=
| |2a+a2+3| | ||
|
| |a2+2a+3| | ||
2
|
| |(a+1)2+2| | ||
2
|
| 2 | ||
2
|
| ||
| 2 |
可得当a=-1时,半径r最小,
∴所有的圆中,面积最小圆的半径r=
| ||
| 2 |
| 1 |
| 2 |
因此,所求圆的方程为(x+1)2+(y-
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 满足
满足 ,求
,求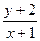 的取值范围。
的取值范围。