题目内容
过抛物线y2=4x的焦点F的直线与抛物线相交于A，B两点，自A，B向准线作垂线，垂足分别为A1、B1，则焦点F与以线段A1B1为直径的圆C之间的位置关系是（ ）
| A．焦点F在圆C上 |
| B．焦点F在圆C内 |
| C．焦点F在圆C外 |
| D．随直线AB的位置改变而改变 |
如图，由抛物线定义可知AA1=AF，故∠AA1F=∠AFA1，
又∵AA1∥x轴，
∠AA1F=∠A1Fx，从而∠AFA1=∠A1Fx，同理可证得∠BFB1=∠B1Fx，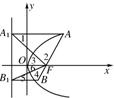
∴∠A1FB1=∠A1FX+∠B1FX=
×π=
，
∴△A1FB1为直角三角形，
∴焦点F与以线段A1B1为直径的圆C之间的位置关系是焦点F在圆C上．
故选A．
又∵AA1∥x轴，
∠AA1F=∠A1Fx，从而∠AFA1=∠A1Fx，同理可证得∠BFB1=∠B1Fx，
∴∠A1FB1=∠A1FX+∠B1FX=
| 1 |
| 2 |
| π |
| 2 |
∴△A1FB1为直角三角形，
∴焦点F与以线段A1B1为直径的圆C之间的位置关系是焦点F在圆C上．
故选A．
练习册系列答案
相关题目