题目内容
已知A、B为两定点,动点M到A与到B的距离比为常数λ,求点M的轨迹方程,并注明轨迹是什么曲线.
点M的轨迹方程是x2+y2+ x+a2=0
x+a2=0 点M的轨迹是以(-
点M的轨迹是以(- ,0)为圆心,
,0)为圆心,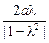 为半径的圆.
为半径的圆.
 x+a2=0
x+a2=0 点M的轨迹是以(-
点M的轨迹是以(- ,0)为圆心,
,0)为圆心,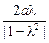 为半径的圆.
为半径的圆. 建立坐标系如图所示,
设|AB|=2a,则A(-a,0),B(a,0).
设M(x,y)是轨迹上任意一点.
则由题设,得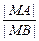 =λ,坐标代入,得
=λ,坐标代入,得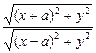 =λ,化简得
=λ,化简得
(1-λ2)x2+(1-λ2)y2+2a(1+λ2)x+(1-λ2)a2=0
(1)当λ=1时,即|MA|=|MB|时,点M的轨迹方程是x=0,点M的轨迹是直线(y轴).
(2)当λ≠1时,点M的轨迹方程是x2+y2+ x+a2=0
x+a2=0 点M的轨迹是以(-
点M的轨迹是以(- ,0)为圆心,
,0)为圆心,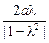 为半径的圆.
为半径的圆.

设|AB|=2a,则A(-a,0),B(a,0).
设M(x,y)是轨迹上任意一点.
则由题设,得
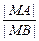 =λ,坐标代入,得
=λ,坐标代入,得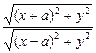 =λ,化简得
=λ,化简得(1-λ2)x2+(1-λ2)y2+2a(1+λ2)x+(1-λ2)a2=0
(1)当λ=1时,即|MA|=|MB|时,点M的轨迹方程是x=0,点M的轨迹是直线(y轴).
(2)当λ≠1时,点M的轨迹方程是x2+y2+
 x+a2=0
x+a2=0 点M的轨迹是以(-
点M的轨迹是以(- ,0)为圆心,
,0)为圆心,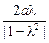 为半径的圆.
为半径的圆. 
练习册系列答案
相关题目
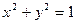 上任意一点,∠AOP的平分线交PA于M(O为原点),试求点M的轨迹.
上任意一点,∠AOP的平分线交PA于M(O为原点),试求点M的轨迹.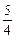 )、N(-4,
)、N(-4,
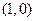 ,且总与直线
,且总与直线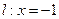 相切.
相切.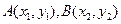 两点,当
两点,当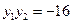 时,
时,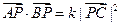 .
.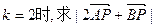 的最大值和最小值.
的最大值和最小值. 和
和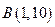 且与直线
且与直线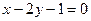 相切的圆的方程。
相切的圆的方程。