题目内容
【题目】如图，棱柱ABCD﹣A1B1C1D1的底面是菱形．侧棱长为5，平面ABCD⊥平面A1ACC1 ， AB=3 
，∠BAD=60°，点E是△ABD的重心，且A1E=4． 
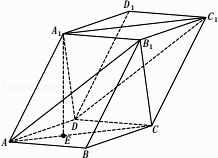
（1）求证：平面A1DC1∥平面AB1C；
（2）求二面角B1﹣AC﹣B的余弦值．
【答案】
（1）证明：因为AA1平行等于CC1，所以四边形A1ACC1是平行四边形，所以A1C1∥AC．
又因为AD平行等于B1C1，所以四边形ADC1B1是平行四边形，所以AB1∥DC1．
因为AC，AB1平面A1DC1，A1C1，DC1平面A1DC1，
所以AC∥平面A1DC1，AB1∥平面A1DC1，又因为AC∩AB1=A，AC，AB1平面AB1C，
所以平面A1DC1∥平面AB1C
（2）解：（2）设AC∩BD=O，由题意可知△ABD是等边三角形．
因为 
，所以 
，
所以 
，所以 
，所以A1E⊥AC，
又因为平面ABCD⊥平面A1ACC1，平面ABCD∩平面A1ACC1=AC，A1E平面A1ACC1，所以A1E⊥平面ABCD．
以E为原点，分别以AC，A1E所在直线为x，z轴，以过点E与BD平行的直线为y轴建立空间直角坐标系，
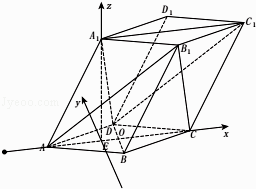
则 
．设B1（x1，y1，z1）．
因为 
， 
， 
，所以 
．
由A1E⊥平面ABCD，可知平面ABCD的法向量是 
．
设平面B1AC的法向量是 
，而 
， 
．
由 
，所以 
．
所以 
．
取平面B1AC的法向量 
，所以 
．
故二面角B1﹣AC﹣B的余弦值为 
【解析】（1）推导出四边形A1ACC1是平行四边形，从而A1C1∥AC．进而四边形ADC1B1是平行四边形，从而AB1∥DC1 ， 进而AC∥平面A1DC1 ， AB1∥平面A1DC1 ， 由此能证明平面A1DC1∥平面AB1C．（2）设AC∩BD=O，推导出A1E⊥AC，从而A1E⊥平面ABCD．以E为原点，分别以AC，A1E所在直线为x，z轴，以过点E与BD平行的直线为y轴建立空间直角坐标系，利用向量法能求出二面角B1﹣AC﹣B的余弦值．
【考点精析】掌握平面与平面平行的判定是解答本题的根本，需要知道判断两平面平行的方法有三种:用定义；判定定理；垂直于同一条直线的两个平面平行．
