题目内容
【题目】设M=10a2+81a+207,P=a+2,Q=26﹣2a,若将lgM,lgQ,lgP适当排序后可构成公差为1的等差数列{an}的前三项. (Ⅰ)求a的值及{an}的通项公式;
(Ⅱ)记函数 ![]() 的图像在x轴上截得的线段长为bn , 设
的图像在x轴上截得的线段长为bn , 设 ![]() ,求Tn .
,求Tn .
【答案】解:(Ⅰ)依题意有﹣2<a<13, ∵M﹣P=10a2+80a+205>0,M﹣Q=10a2+83a+181>0,
∴M最大.
又P﹣Q=﹣24+3a,
当﹣2<a<8时,P<Q,lgP+1=lgQ.
∴10P=Q,
∴ ![]() ,此时M>Q>P,且满足lgM=1+lgQ.
,此时M>Q>P,且满足lgM=1+lgQ.
∴ ![]() 符合题意.
符合题意.
当8<a<13时,P>Q,lgP=1+lgQ.
∴10Q=P,
∴ ![]() .
.
但此时不满足lgM=1+lgP.
∴ ![]() .
.
∴{an}的前三项为lgP,lgQ,lgM,此时 ![]() .
.
∴an=lgP+(n﹣1)×1=n﹣2lg2.
(Ⅱ)∵2an+1=an+an+2
∴x=﹣1是函数 ![]() 的零点
的零点
即f(x)=0时,(x+1)(anx+an+2)=0
∴ 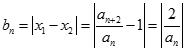 ,||bn=|x1﹣x2|=
,||bn=|x1﹣x2|= 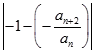
又∵an=n﹣2lg2>0,
∴ ![]() ,
,
∴ 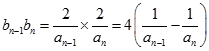 .
.
∴ 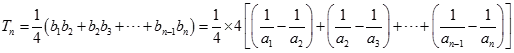
= ![]()
= ![]()
【解析】(Ⅰ)依题意有﹣2<a<13,利用作差法可比较M,P,Q中M最大,而P,Q的大小需要根据a的范围来确定,结合等差数列及对数的运算性质可求出满足题意的a及通项(Ⅱ)由等差数列的性质可得,2an+1=an+an+2 , 由f(x)=0时,(x+1)(anx+an+2)=0,从而可求得 ![]() ,结合an=n﹣2lg2>0,可得bn , 然后代入,利用裂项求和即可
,结合an=n﹣2lg2>0,可得bn , 然后代入,利用裂项求和即可
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系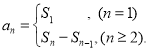 ),还要掌握等差数列的性质(在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列)的相关知识才是答题的关键.
),还要掌握等差数列的性质(在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列)的相关知识才是答题的关键.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案