题目内容
【题目】各项均为正数的等差数列{an}前n项和为Sn ， 首项a1=3，数列{bn} 为等比数列，首项b1=1，且b2S2=64，b3S3=960．
（1）求an和bn；
（2）设f（n）= 
（n∈N*），求f（n）最大值及相应的n的值．
【答案】
（1）解：设等差数列{an}的公差为d，等比数列{bn}的公比为q，则d＞0，
∴ 
，
依题意： 
，解得 
或 
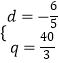（舍）．
∴an=2n+1， 
；
（2）解：∵Sn=n（n+2），
∴f（n）= 
= 
≤ 
．
当且仅当n= 
，即n=10时取等号．
∴当n=10时，所求最小值为 
【解析】（1）设出等差数列的公差和等比数列的公比，由已知列式求得等差数列的公差和等比数列的公比，则an和bn可求；（2）把等差数列{an}的通项和前n项和为Sn代入f（n）= ，整理后利用基本不等式求得f（n）最大值及相应的n的值．
练习册系列答案
相关题目
