题目内容
【题目】抛物线y2=4x的焦点为F，过点（0，3）的直线与抛物线交于A，B两点，线段AB的垂直平分线交x轴于点D，若|AF|+|BF|=6，则点D的横坐标为 ．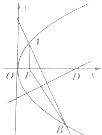 
【答案】4
【解析】解：设AB的中点为H，
抛物线y2=4x的焦点为F（1，0），准线为x=﹣1，
设A，B，H在准线上的射影分别为A'，B'，H'，
则|HH'|= 
（|AA'|+|BB'|），
由抛物线的定义可得，
|AF|=|AA'|，|BF|=|BB'|，
|AF|+|BF|=6，即为|AA'|+|BB'|=6，
|HH'|= ×6=3，
即有H的横坐标为2，
设直线AB：y=kx+3，
代入抛物线方程，可得k2x2+（6k﹣4）x+9=0，
即有判别式（6k﹣4）2﹣36k2＞0，解得k＜ 
且k≠0，
又x1+x2= 
=4，
解得k=﹣2或 （舍去），
则直线AB：y=﹣2x+3，
AB的中点为（2，﹣1），
AB的中垂线方程为y+1= （x﹣2），
令y=0，解得x=4，
则D（4，0）．
所以答案是：4．
练习册系列答案
相关题目
