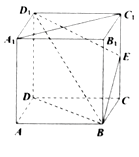
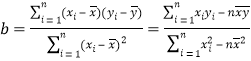��Ŀ����
����Ŀ��ijУΪ�����һ���߶�ѧ�������ڼ�ѧϰ��ʱ����������ȡ�˸�һ���߶���![]() �ˣ������ǵ�ѧϰʱ�������ͳ�ƣ��ֱ�õ��˸�һѧ��ѧϰʱ�䣨��λ��Сʱ����Ƶ���ֲ����߶�ѧ��ѧϰʱ���Ƶ�ʷֲ�ֱ��ͼ.
�ˣ������ǵ�ѧϰʱ�������ͳ�ƣ��ֱ�õ��˸�һѧ��ѧϰʱ�䣨��λ��Сʱ����Ƶ���ֲ����߶�ѧ��ѧϰʱ���Ƶ�ʷֲ�ֱ��ͼ.
��һѧ��ѧϰʱ���Ƶ���ֲ�����ѧϰʱ���������![]() �ڣ���
�ڣ���
ѧϰʱ�� |
|
|
|
|
|
|
Ƶ�� | 3 | 1 | 8 | 4 | 2 | 2 |
�߶�ѧ��ѧϰʱ���Ƶ�ʷֲ�ֱ��ͼ��
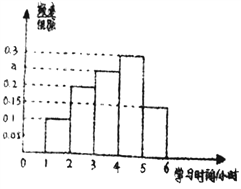
��1����߶�ѧ��ѧϰʱ���Ƶ�ʷֲ�ֱ��ͼ�е�![]() ֵ�������ݴ�Ƶ�ʷֲ�ֱ��ͼ���Ƹ�У�߶�ѧ��ѧϰʱ�����λ����
ֵ�������ݴ�Ƶ�ʷֲ�ֱ��ͼ���Ƹ�У�߶�ѧ��ѧϰʱ�����λ����
��2�����÷ֲ�����ķ������Ӹ�һѧ��ѧϰʱ����![]() ��
��![]() �������������ȡ
�������������ȡ![]() �����ٴ���
�����ٴ���![]() ���������ȡ
���������ȡ![]() ������ѧϰʱ����
������ѧϰʱ����![]() ��һ����������
��һ����������![]() �˱����еĸ���.
�˱����еĸ���.
���𰸡���1��![]() ��3.8����2��
��3.8����2��![]()
����������������1���������ʷֲ�ֱ��ͼ��������ֱ��ͼ�����֮��Ϊ1�ɵ�aֵ����2�����ݷֲ��������ɵã��Ӹ�һѧ��ѧϰʱ����![]() �г�ȡ
�г�ȡ![]() �ˣ��Ӹ�һѧ��ѧϰʱ����
�ˣ��Ӹ�һѧ��ѧϰʱ����![]() �г�ȡ
�г�ȡ![]() �ˣ�
�ˣ�
Ȼ����ݹŵ���ͼ��㹫ʽ�ɵý���.
��⣺
��1����ͼ��֪��ѧ��ѧϰʱ��������![]() �ڵ�Ƶ��Ϊ
�ڵ�Ƶ��Ϊ![]() ��
��
![]() �ڵ�Ƶ��Ϊ
�ڵ�Ƶ��Ϊ![]() ������
������![]()
����λ��Ϊ![]() ����
����![]() �����
�����![]() ��
��
����У�߶�ѧ��ѧϰʱ�����λ��Ϊ![]() .
.
��2�����ݷֲ�������Ӹ�һѧ��ѧϰʱ����![]() �г�ȡ
�г�ȡ![]() �ˣ��Ӹ�һѧ��ѧϰʱ����
�ˣ��Ӹ�һѧ��ѧϰʱ����![]() �г�ȡ
�г�ȡ![]() �ˣ�����
�ˣ�����![]() ���������ȡ
���������ȡ![]() �˹���
�˹���![]() �����������ѧϰʱ����
�����������ѧϰʱ����![]() ��һ����û�˱����е���
��һ����û�˱����е���![]() �����������
�����������![]() ��һ����������
��һ����������![]() �˱����е��¼�Ϊ
�˱����е��¼�Ϊ![]() ��
��
��![]() .
.